最长回文子串
问题定义
给出一个字符串,找出其中的最长回文子串。
“回文串”是指,这个字符串从前往后读,和从后往前读效果是一样的。
比如”testset”、”hahaschooloohcsahah”,这样的串都是回文串。
子串是指在字符串中抽出的一段连续的字符,比如”school”是”hahaschool”的一个子串,”hsol”并不是”hahaschool”的子串,因为在原串中的对应位置不连续,”poi”也不是”hahaschool”的子串,因为无法在原始串中无法找到’p’和’i’。
朴素解法
解法一
枚举最长的回文串的长度len,在原始串中枚举len长度的子串,然后判断该子串是否为回文串,如果是的话更新答案。
时间代价:枚举长度O(n) * 枚举子串O(n) * 判断回文O(n) –> O(n^3)
解法二
枚举最长回文子串的中心center,然后尝试扩张以center为中心的回文子串(检查两边的字符是否相等,是的话扩张,否则停止)到最大,然后更新答案。
时间代价:枚举中心O(2n)=O(n) * 扩张O(n) –> O(n^2)
优化解法
解法三
分奇偶二分最长回文子串长度len。
检查len是否可行的方法是:然后枚举len长度的回文串的中心位置,然后判断是否回文。
时间代价:二分答案O(2logn)=O(logn) * 检查可行性O(n) * 回文判断O(n) –> O(n^2 logn)
看起来比解法二还慢,我们可以再加一个优化:利用Rabin-Karp方法哈希原始串和原始串反向串,通过判断回文串的左半部分的哈希值是否等于反向的右半部分哈希值,就可以判断是否回文,这样就可以实现回文判断的O(1)。
时间代价: 二分答案O(2logn)=O(logn) * 检查可行性O(n) * 回文判断O(1) –> O(n logn)
解法四
首先,回文子串的左半部分是原始串的一个后缀,右半部分是原始串的反向串的一个后缀。
使用后缀数组,首先把原始串和原始串的反向串中间用一个特殊字符(只要字符串中没有出现过就可以,比如’#’)链接,然后求出链接后的串的后缀数组和LCP数组(height)。
接下来,只要枚举回文串的中心center,然后在利用LCP数组查询center对应的原始串后缀和反串后缀的LCP即可。
时间代价:后缀数组O(nlogn)或O(n) + 枚举中心O(n) * 求LCP O(logn) –> O(nlogn)
解法五
就是我们接下来要讨论的Manacher算法,可以达到O(n)的时间复杂度下界。
Manacher算法
开始之前的一些定义
- 我们的数组下标都是从0开始
- 我们接下来将称呼原始串为T
- 我们知道,回文子串的中心位置可能是一个字符本身,也可能是两个字符之间的空隙,所以我们接下来将把T做一些改动,即在每个字母的前后插入一个特殊字符’|’来表示字符间的空隙,如”abababa”,将会变成”|a|b|a|b|a|b|a|”,我们令这个改动后的串为S。简单观察一下,我们就可以发现,S的长度len(S) = len(T) * 2。
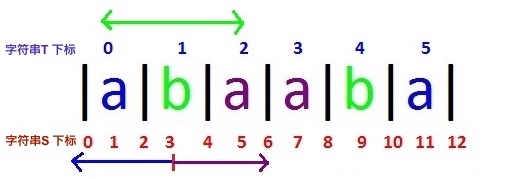
- 我们定义数组rad[],rad[center]表示以center为中心的回文串的回文半径,其中center对应S的下标。举个例子,”|a|b|a|b|a|”,rad[0] = 0(分割线暂时忽略),rad[1] = 1(“a”构成回文),rad[5] = 5(“a|b|a|b|a”构成回文)。
为了更好地理解上述定义,再附两个例子:


我们接下来的目标就是在线性时间内算出rad[]的值。
先来找找规律
先来看一个例子:”abaaba”
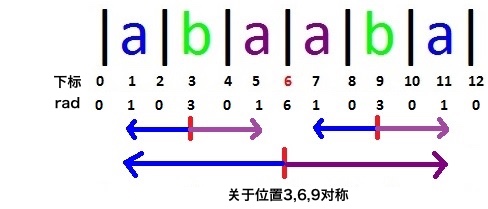
观察图中标示出来的回文子串,发现什么了?
- rad[2] = rad[4] = 0
- rad[1] = rad[5] = 1
如果我们知道了rad[1]、rad[2]、rad[3]的值,那么我们就不用再去算rad[4]和rad[5]了,因为它们等于子串中心3左边的对应的点的rad值。
然后再观察以6为中心的回文子串,你会发现:
- rad[5] = rad[7]
- rad[4] = rad[8]
- …
也就是说如果我们已经知道了rad[1~6]的值,rad[7~11]的值就不用额外算了,他们都可以对应到以6为中心的回文串的左半部分。
那我们再来看一个例子:”abababa”
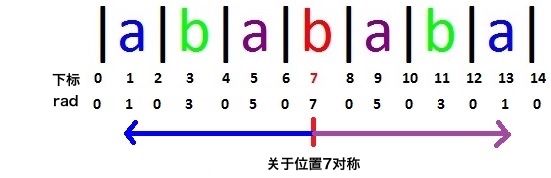
按照上个例子那样,注意图中的标示,我们发现rad[1~6]可以和rad[8~13]对应上。
看起来在回文串的中心两边的rad值是对称的。然而这一点并不是一直成立
。我们注意当前这个例子的位置3和位置11,我们发现这两个位置对应的回文串内部并没有刚才那样的对称关系。
这给了我们一个提示,也许有没有这种对称关系取决于某种条件,当这种条件满足的时候,就可以通过对称关系来减少计算量,从而达到线性时间复杂度。如果条件不满足的话,就需要暴力判断。
那么我们接下来的目标就是探索这个规律。
在深入问题之前的补充定义
在深入问题之前,需要补充一些新的定义:
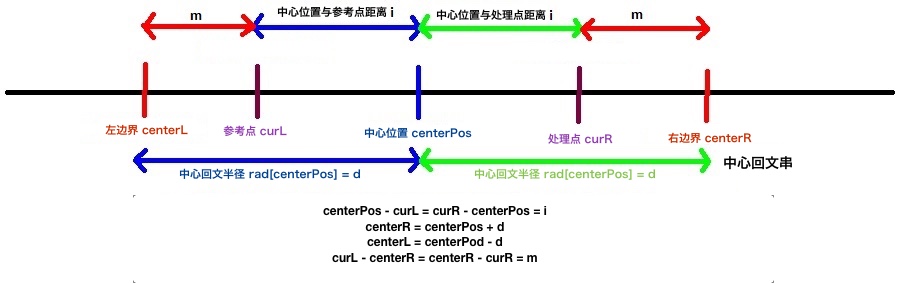
- 中心位置centerPos:在中心位置的rad已经算好,我们令rad[centerPos]为d
- 右边界centerR:在中心位置右侧距离中心位置d单位远的位置,即中心位置所示的回文串的右边界,centerR = centerPos + d
- 左边界centerL:在中心位置左侧距离中心位置d单位远的位置,即中心位置所示的回文串的右边界,centerR = centerPos – d
- 当前处理位置curR:在中心位置右边,我们需要求rad值的位置
- 当前参考位置curL:在中心位置左边,我们已经求好了rad值的位置
- 我们发现有这样的几个等式:
- centerPos – curL = curR – centerPos
- centerL = 2*centerPos – curR
- i-左回文串:中心距离centerPos i单位远的左侧的回文串,即以curL为中心的回文串
- i-右回文串:中心距离centerPos i单位远的右侧的回文串,即以curR为中心的回文串
- 中心回文串:中心位置对应的回文串
深入问题
当我们处在中心位置centerPos的时候,我们之前已经求出了centerPos及之前所有位置的rad值了,这也意味着centerPos-d到centerPos+d是一个回文串。我们现在要处理curR位置,即算出rad[curR]。
我们需要一点分类讨论,首先是:
情形1:
i-左字符串被真包含(没有碰到中央回文串边界)于中心回文串内,且i-左字符串不是中心回文串的后缀,则有rad[curR] = rad[curL],即:
我们来考虑”abababa”这个例子:
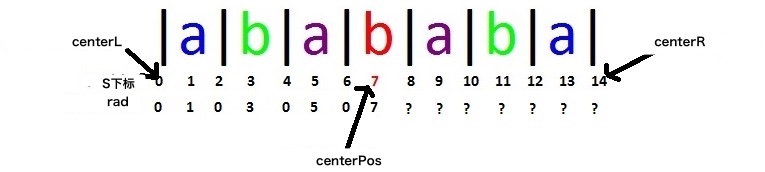
我们现在已经算出了rad[0~7],中心位置 centerPos = 7,对应回文串半径 rad[centerPos] = d = 7,左边界 centerL = 0, 右边界 centerR = 14。接下来我们要去算8及之后的rad值。
对于curR = 8,有curL = 6,和rad[curL] = 0,同时有 centerR – curR = 14 – 8 = 6,这符合情形1,所以我们有rad[curR] = rad[curL] = 0。
接下来对于curR = 10和curR = 12,也适用情形1。它们分别有:
- rad[10] = rad[4] = 0
- rad[1] = rad[2] = 0
然后,我们来看位置9,我们有:curR = 9, curL = 5,centerR – curR = 5。
这里我们有rad[curL] = centerR – curR,也就是说情形1并不适用。我们同时注意到了centerR是整个字符串的末尾,这也就意味着中心回文串是输入的字符串的后缀。也就是:
情形2:
当i-左回文串是中心回文串的前缀且中心回文串是输入字符串的后缀时,rad[curR] = rad[curL]。即:
位置9、11、13、14都适用情形2,我们有:
- rad[0] = rad[5] = 5
- rad[11] = rad[3] = 3
- rad[13] = rad[1] = 1
- rad[14] = rad[0] = 0
情形1和情形2的原理其实就是利用了回文串的性质,当一个较小的回文串被包含在一个较大的回文串中,且小回文串的中心在大回文串的左半部分时,根据回文串的对称性,大回文串应该有和左半部分相同的另外一个小回文串,中心在右半部分。
在情形1中,右边的回文串一定等于左边的回文串,否则如果右边的回文串能够扩张,左边的回文串也必然能够扩张,因为左边的回文串被真包含于大回文串之内(没有碰到大回文串边界),扩张时新加的字母也一定出现在了大回文串的右侧,扩张了右边的回文串,所以左边等于右边,反之亦然。
在情形2中,虽然左边的回文串是大回文串的前缀,如果右边发生扩张,不能保证对应的字母出现在左边,然而根据我们的条件,右边正好是整个输入字符的后缀,也就是右边的回文串根本不可能延长,所以左边等于右边。
上述的两种情形我们可以直接得出rad[curR]的值,不需要别的计算。
此外,还有两种情形:
情形3:
当i-左回文串是中心回文串的前缀且中心回文串不是输入字符串的后缀时,rad[curR] >= rad[curL]。即:
情形3基于情形2,情形2的右边回文串是不能加字符扩张的,而情形3可以。当右边的回文串加字符扩张后,左边的回文串并不能扩张,因为新加的字符在中心回文串的外面,这个字符没有对应到左边去。
情形3只是给rad[curR]提供了一个下界,接下来我们需要暴力检验才能得到真实的rad[curR],不过这依然减少了运算量。
情形4:
当i-左回文串与中心回文串交叉时,rad[curR] >= centerR – curR。即:
当我们的中心回文串不能覆盖左边回文串的时候,我们不妨缩小左边回文串到中心回文串能覆盖的程度,这样一来就和情形3是一样的了。
经过了以上四种情形的分类讨论,我们覆盖了所有在处理rad[curR]中可能出现的情况。
接下来我们基于这种思路来做实现。
实现
这份实现严格遵守了上面的思路,但是比较复杂,不太适合在实战中使用。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
#define MANACHER_TUTORIAL #ifdef MANACHER_TUTORIAL namespace Manacher{ const int MAXN = 1005; char str[MAXN]; int rad[MAXN];//回文半径 void manacher(){ int len = strlen(str); len = (len << 1) + 1; rad[0] = 0,rad[1] = 1; int centerPos = 1;//当前回文串中心位置 int centerR = 2;//当前回文串右边界 int curR = 0;//当前正在处理的点(右部) int curL;//用于参考的点(左部) int maxLPS = 0,maxPOS = 0; int diff = -1,expand = -1; for(curR = 2;curR < len; curR++){ //计算出参考点位置 curL = 2*centerPos - curR; //重置扩张计数 expand = 0; diff = centerR - curR; if(diff > 0){ if(rad[curL] < diff){ //情形1 rad[curR] = rad[curL]; }else if(rad[curL] == diff && curR == len-1){ //情形2 rad[curR] = rad[curL]; }else if(rad[curL] == diff && curR < len-1){ //情形3 rad[curR] = rad[curL]; expand = 1; }else if(rad[curR] > diff){ //情形4 rad[curR] = diff; expand = 1;//需要扩张curR为中心的回文串 } }else{ rad[curR] = 0; expand = 1;//需要扩张curR为中心的回文串 } if(expand == 1){ //尝试扩张以curR为中心的回文串 //对于奇数的位置,需要比较字符是否相等来决定能否扩张 //对于偶数的位置,直接扩张 while(true){ if((curR + rad[curR] < len) && (curR - rad[curR] > 0)); else break;//达到了字符串边界,停止扩张 if((curR + rad[curR] + 1)&1)//奇数位置的情形:需要判断字符相等 if(str[(curR + rad[curR] + 1)/2] == str[(curR - rad[curR] - 1)/2]) rad[curR]++; else break;//无法匹配字符,停止扩张 else rad[curR]++;//偶数位置的情形,直接扩张 } } if(curR + rad[curR] > centerR){ //如果curR对应的回文串扩张到了centerPos对应的回文串的外面 //我们要移动centerPos到curR位置上,并算出新的右边界centerR centerPos = curR; centerR = curR + rad[curR]; } } } } #endif |
简化实现
观察一下我们分析的4种情形,我们会发现其实没有必要写那么繁琐,我们可以从下面几个方面减轻代码负担:
- 我们没必要计算S数组对应于T数组的位置,直接把S数组当作目标即可。
- 前3种情形都是令rad[curR] = rad[curL],第四种情形是令rad[curR] = centerR – curR,我们不妨直接令rad[curR] = min(rad[curL], centerR – curR)。
- 对于情形1,2,不需要扩张,但我们尝试扩张也没什么关系。
这样,我们可以把上面的一大堆缩减到这样的程度:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
#define MANACHER #ifdef MANACHER namespace Manacher{ /* Manacher Algorithm. MAXN : Maximum string length. rad : Maximum panlidrome radius. <0,MAXN> tmp : Alternated string for manacher working process. <0,2*MAXN> Example: hahaschool --> *#h#a#h#a#s#c#h#o#o#l#$ ($ being '\0') #define REP(i,t) for(int i = 0;i < t; i++) #define REP_1(i,t) for(int i = 1;i <= t; i++) Time : O(n) Space : 3n */ const int MAXN = 1005; char tmp[MAXN*2]; int rad[MAXN]; void manacher(char *str){ memset(tmp, 0, sizeof(tmp)); //将原始字符串插入辅助字符(必须确保下述两个辅助字符没有在字符串中出现过) tmp[0] = '*', tmp[1] = '#'; int len = strlen(str); REP(i, len){ tmp[i*2+2] = str[i]; tmp[i*2+3] = '#'; } len = (len+1)<<1; tmp[len] = 0; //Manacher主过程 //id:当前回文串中心 ma:当前回文串右边界 int id = 0,ma = 0; REP_1(i, len-1){//正在处理的右部点 if(ma > i) rad[i] = min(ma-i,rad[id*2-i]);//拉取当前回文串的"基本长度" else rad[i] = 1;//当前处理中心已经超出右边界,只能暴力扩张 while(tmp[i-rad[i]] == tmp[i+rad[i]]) rad[i]++;//尝试扩张以i为中心的回文串 if(i + rad[i] > ma){//当以i为中心的回文串超出右边界,要更改中心点和算出新的右边界 id = i; ma = i + rad[i]; } } } } #endif |
不刻意压行就可以达到简短的20行代码,非常简洁好记。
应用举例
裸题
左端点对应最长回文串
结合线段树
参考文献与致谢
- Anurag Singh from GeeksforGeeks for pictures and some ideas.
- doubility::Zhenkun Csi for beautiful implementation in C++.