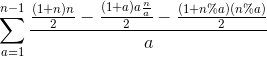给你一个数n，n不能被2,5整除，问你n的最小的每个数位全是1的倍数有多少位。
同余定理，另外这个题保证有解，所以相信自己，暴力出奇迹。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
#include <cstdio> int main(){ int n = 0; while (scanf(" %d",&n) != EOF) { int cnt = 1; int base = 1; base %= n; while (base != 0) { base = ((base * 10)%n+1%n)%n; cnt++; } printf("%d\n",cnt); } return 0; } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 |
#include <iostream> #include <algorithm> #include <queue> #include <vector> #include <cstdlib> #include <cstdio> #include <string> #include <cstring> #include <ctime> #include <iomanip> #include <cmath> #include <set> #include <stack> #include <cmath> using namespace std; #define MAXN 262145 int tree[MAXN]; int lazy[MAXN]; int mark[MAXN]; int M = 1,H = 0; void tree_init(unsigned int num){ memset(tree, 0, sizeof(tree)); memset(lazy, 0, sizeof(lazy)); memset(mark, 0, sizeof(mark)); M = 1; for (; M < num+2; M <<= 1) H++; M--; for (int i = 1; i <= num; i++) { mark[i+1+M] = 1; } for (int i = M; i >= 1; i--) { mark[i] = mark[(i << 1) + 1] + mark[i << 1]; } } void lazy_down(int pos){ if (lazy[pos]) { lazy[pos] = 0; lazy[pos*2] = lazy[pos*2]?0:1; tree[pos*2] = mark[pos*2] - tree[pos*2]; lazy[pos*2+1] = lazy[pos*2+1]?0:1; tree[pos*2+1] = mark[pos*2+1] - tree[pos*2+1]; } } void tree_negate(int from,int to,int l,int r,int pos){ //default pos = 1 l = 1 r = n if (r < from || l > to){ //out of range return; }else if (l >= from && r <= to) { //fully inclusive lazy[pos] = lazy[pos]?0:1; tree[pos] = mark[pos] - tree[pos]; }else{ //partially inclusive lazy_down(pos); tree_negate(from, to, l, l+mark[pos*2]-1, pos*2); tree_negate(from, to, l+mark[pos*2], r, pos*2+1); if (l < r) { tree[pos] = tree[pos*2] + tree[pos*2+1]; } } } int res; void tree_query(int from,int to,int l,int r,int pos){ //default pos = 1 l = 1 r = n if (r < from || l > to){ //out of range return; }else if (l >= from && r <= to) { //fully inclusive res += tree[pos]; }else{ //partially inclusive lazy_down(pos); tree_query(from, to, l, l+mark[pos*2]-1, pos*2); tree_query(from, to, l+mark[pos*2], r, pos*2+1); } } int n = 0,m = 0; vector<int> child[MAXN]; vector<int> linear; int str[MAXN],ter[MAXN]; bool vis[MAXN]; void dfs(int cur){ linear.push_back(cur); str[cur] = (int)linear.size(); vis[cur] = true; for (int i = 0; i < child[cur].size(); i++) { if (!vis[child[cur][i]]) { dfs(child[cur][i]); } } ter[cur] = (int)linear.size(); } int main(){ while (scanf(" %d %d",&n,&m) != EOF) { tree_init(n); for (int i = 1; i <= n; i++) { child[i].clear(); } for (int i = 2; i <= n; i++) { int parent; scanf(" %d",&parent); child[parent].push_back(i); } memset(vis, false, sizeof(vis)); linear.clear(); dfs(1); for (int i = 1; i <= m; i++) { char arg1; int arg2; scanf(" %c %d",&arg1,&arg2); if (arg1 == 'o') { tree_negate(str[arg2], ter[arg2], 1, n, 1); }else{ res = 0; tree_query(str[arg2], ter[arg2], 1, n, 1); printf("%d\n",res); } } printf("n"); } return 0; } |
被这道题玩得相当惨。。。这道题是一个DFS＋线段树的题。
首先这个题是在一棵传统树上面进行大规模的区间读写操作，这是线段树的玩法，但是怎么玩呢？
这个时候DFS就派上用场了，我们通过DFS得到DLR遍历，把dfs时进入一个节点是时间记下来，出去一个节点的时间记下来，就可以得到这个节点的子树在DLR遍历中的区间的开始与结束标号，这样就相当于把2维的树降到一维了。
之后得到了一个一维的数组，就可以开线段树，这里涉及区间更新，还要加开懒惰标记。
这种把树压成线然后再搞是一种很常用很好的姿势！
其实这道题卡死我的就是懒惰标记这里。我原来一直在用zkw线段树，但是因为是自下向上操作没有递归，所以我就根本不知道怎么下手写懒惰标记了，鼓捣2天未果，orz各路大神的适配zkw线段树的懒惰标记是给rmq准备的，不适合这个题，没办法研究递归版本了。
递归版本的话，实现懒惰标记的思路就是：
1.更新时，如果发生了目标区间与当前区间相交的情况，首先把当前节点的懒惰标记下传给下一层，然后再去更新下一层，更新完下一层后，用更新好的下一层更新自身。如果目标区间完全包括当前区间，这个时候就不用往下走了，首先更新自己的值，然后更新自己位置的懒惰标记。
2.查询时，如果目标区间和当前区间相交，这时候需要下传当前节点的懒惰标记，然后进入下一层接着查询，如果目标区间完全包括当前区间，直接更新答案。
3.下传时，我们只操作当前节点的子节点，不可以操作当前节点（否则就重复操作啦），注意我们只下传了一层，所以不仅要操作下面一层的值，还要操作下面一层的懒惰标记，同时清空当前节点的懒惰标记。
这个题很不错，卡了我半星期，再加上这个题没有题解，所以这次认真一些,因为不会LaTeX，这个题解写着挺吃力的。
题意
给定一个集合，这个集合的内容一定是{1,2,3,…,n}这个样子，要你求出这个集合的子集中，自成等差数列的有多少个。
举个例子，给出n=4，那么集合为{1,2,3,4},符合要求的子集有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3},{2,3,4},{1,2,3,4},一共有9个，输出9就可以了。
AC做法
特别感谢cos65535的题解（日文）。cos65535さん、ありがとうございます！
这里我来说明一下这个做法，对于一个给定的n，一共有1～n-1这些可能的公差，对于每个公差a，形成的等差数列最多有（(n-1)/a)＋1项，也就是最多可以扣掉(n-1)/a个公差。扣掉b个公差的话，可以最多形成n-ab个等差数列。
在这里举个例子来说明这个，给出一个n=8，求公差为3的情况，那么可以算出对于8，可以扣掉最多2个3保证等差数列的起点不出界。扣掉一个3的时候，形成2项的等差数列，这个等差数列的终点最大为8，也就是{5,8}，把这个数列整个减1，这样就得到{4,7}{3,6}{2,5},{1,4}，一共是5个（8-1*3），同样地扣掉两个3的时候，形成3项的等差数列，终点最大为8，即{2,5,8}，像刚才那样整体减1，得到{1,4,7}，一共是2个(8-2*3).2+5=7,这个就是公差3的时候可以组成的等差数列数目了。
这个方法写成公式很简单，就是
。
但是光有这个公式还不够，因为题目的数据范围是10^9,而上面介绍的那个做法是O(n^2)的时间复杂度，超时不可避啊。
优化需要两次，第一次是当公差一定时，我们可以用等差数列求和公式一次性求出来当前公差可以得到的当差数列数量。第二次是当我们使用完等差数列求和公式后，我们发现得到的式子中出现了n/a的形式，对于一定的n，a<=n,一共有sqrt(n)个n/a值（整数除法的特点），利用这一特点，我们可以只枚举1～sqrt(n-1)，我用这个范围枚举的是“最大可扣掉公差数目b”，对于给定的b，它适用于公差从(n-1)/b到(n-1)/(b+1)的情况，这里我们改造一下之前等差数列求和优化好的式子，再用一次等差数列求和。同时不要忘了我们的b值只枚举到了sqrt(n-1),每一次算出(n-1)/b其实就是对应的sqrt(n-1)以上的只对应一个公差的b值。
接下来上代码：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
#include <cstdio> #include <iostream> #include <cmath> using namespace std; #define MODER 100000007 int main(){ long long n = 0; while (scanf(" %lld",&n) != EOF) { long long res = 0; long long b = 1; for (long long a = n-1; b <= sqrt(n-1);) { long long c = (n-1)/b - (n-1)/(b+1); //cout << a << '|' << b << "~" << c << endl; res += n*b*c-((a+a-c+1)*c/2)*b*(1+b)/2; if(!(a==b)) res += n*a-b*a*(1+a)/2; res %= MODER; b++; a = (n-1)/b; } printf("%lld\n",res); } return 0; } |
递推方法
感谢于济凡同学。
对于1～n这个集合的满足要求的子集数目，设定为f(n)，对于n－1这个数，小于等于它的数中可以整除它的数的数量设定为g(n)，我们有递推关系式f(n)=2f(n-1)-f(n-2)+g(n)
这里说明思路，{1,2,…,n}这个集合，我们可以看成是{1,…,n-1}这个集合组成的全部等差数列，加上{2,…,n}这个集合组成的全部等差数列，但是我们发现{2,…,n-1}这个集合的等差数列算了两次，我们要去掉一次，但是我们还是少了一种情况，就是以1开头，n结尾的等差数列数目，这个就是g(n)了。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
#include<iostream> #include<cmath> using namespace std; int f(int t) { int counter=0; for(int i=1;i<=t;i++) { if(t%i==0) counter++; } return counter; } int ans(int n) { if(n==1) return 0; else if(n==2) return 1; else return ans(n-1)*2%100000007-ans(n-2)%100000007+f(n-1)%100000007; } int main() { int m; while(cin>>m) { cout<<ans(m)<<endl; } } |
另一种求等差数列个数的方法
感谢铲神。
已知等差数列的公差、最后一项和首项，藉由等差数列通项公式，我们可以求出可用的等差数列数量。
其中
是公差
是最后一项
是首项，现在是n^2的时间复杂度，接下来优化为下面的形式，为n的时间复杂度，但是怎么弄成sqrt(n)的复杂度我实在想不出来了。。。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
#include <cstdio> #include <iostream> #include <cmath> using namespace std; #define MODER 100000007 int main(){ long long n = 0; while (scanf(" %lld",&n) != EOF) { long long sum = 0; for (long long a = 1; a <= n; a++) { long long tmp =0; tmp += (1+n)*n/2; tmp -= (1+n%a)*(n%a)/2; tmp -= (1+a)*a/2*(n/a); cout << tmp; tmp /= a; cout << '~' << tmp << endl; tmp %= MODER; sum += tmp; sum %= MODER; } printf("%lld\n",sum%MODER); } return 0; } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 |
#include <iostream> #include <algorithm> #include <queue> #include <vector> #include <cstdlib> #include <cstdio> #include <string> #include <cstring> #include <ctime> #include <iomanip> #include <cmath> #include <set> #include <stack> using namespace std; #define MAXN 200005 struct nodeType{ vector<int> to; int dep; } node[MAXN]; void init_node(int n,bool clearljb){ for (int i = 1; i <= n; i++) { if(clearljb) node[i].to.clear(); node[i].dep = 1; } } vector<int> tdr; int prevNode[MAXN]; bool vis[MAXN]; int bfs(int n,bool metaMode,int src,bool gentdr,int blocked){ //0 for meta 1 for tdim //make blocked 0 if you do not want to split init_node(n,false); memset(vis, 0, sizeof(vis)); memset(prevNode, 0, sizeof(prevNode)); queue<int> q; q.push(src); int last = 0,maxdep = 0; while (!q.empty()) { nodeType &now = node[q.front()]; vis[q.front()] = true; if (now.dep > maxdep) { maxdep = now.dep; last = q.front(); } for (int i = 0; i < now.to.size(); i++) { if (vis[now.to[i]] || now.to[i] == blocked) { continue; } node[now.to[i]].dep = now.dep+1; q.push(now.to[i]); prevNode[now.to[i]] = q.front(); } q.pop(); } if (metaMode) { return last; }else { if (gentdr) { tdr.clear(); int tmp = last; while (src != tmp) { tdr.push_back(tmp); tmp = prevNode[tmp]; } tdr.push_back(src); } return maxdep; } } int main(){ int casecnt; cin >> casecnt; while (casecnt--) { int n; cin >> n; init_node(n,true); for (int i = 1; i <= n-1; i++) { int a = 0,b = 0; scanf(" %d %d",&a,&b); node[a].to.push_back(b); node[b].to.push_back(a); } int seed = rand()%n+1; int meta = bfs(n, true, seed,false,0); int tdim = bfs(n, false, meta, true,0); int lans = 0,rans = 0,dis = 0; if (tdim % 2) { vector<int> origtdr = tdr; int center = (tdim-1)/2; //odd situ1 int lmeta1 = bfs(n, true, origtdr[0], false, origtdr[center]); int ltdim1 = bfs(n, false, lmeta1, true, origtdr[center]); int lpos1 = tdr[ltdim1/2]; int rmeta1 = bfs(n, true, origtdr[tdim-1], false, origtdr[center-1]); int rtdim1 = bfs(n, false, rmeta1, true, origtdr[center-1]); int rpos1 = tdr[rtdim1/2]; int judge1 = max(ltdim1/2,rtdim1/2); //odd situ2 int lmeta2 = bfs(n, true, origtdr[0], false, origtdr[center+1]); int ltdim2 = bfs(n, false, lmeta2, true, origtdr[center+1]); int lpos2 = tdr[ltdim2/2]; int rmeta2 = bfs(n, true, origtdr[tdim-1], false,origtdr[center]); int rtdim2 = bfs(n, false, rmeta2, true, origtdr[center]); int rpos2 = tdr[rtdim2/2]; int judge2 = max(ltdim2/2,rtdim2/2); //judge if (judge1 > judge2) { //2 is good lans = lpos2; rans = rpos2; dis = judge2; }else{ //1 is good lans = lpos1; rans = rpos1; dis = judge1; } }else{ //even situ int lend = tdr[tdim/2-1]; int rend = tdr[tdim/2]; //run left int lmeta = bfs(n, true, tdr[0], false,rend); //run right int rmeta = bfs(n, true, tdr[tdim-1], false, lend); int ltdim = bfs(n, false, lmeta, true, rend); lans = tdr[ltdim/2]; int rtdim = bfs(n, false, rmeta, true, lend); rans = tdr[rtdim/2]; dis = max(ltdim/2,rtdim/2); } cout << dis << ' ' << lans << ' ' << rans << ' ' << endl; } return 0; } |
SXBK的一个题（对我现在的水平来说）
其实是这样，对于一棵树，在上面建1个消防站，最优位置在直径中心，建立两个消防站呢？其实可以把整个大树分成两个小树，在每个小树自己的直径的中心建立消防站就搞定了，在分树的时候，如果发生分歧（如果直径有奇数个点，就会出现这种分歧情况，如果有偶数个节点，中央节点有两个，直接从两个节点的中央裂开就行，不会产生分歧），这时候我把中央节点上连接的那些节点中除了直径上的两点之外的那些节点都叫做中立节点，我们只要进行两次讨论，一次把这些中立节点分入左半树，求出这种分法中左右半树的直径，然后把左右直径的最大值当成接下来判定哪个方法更好的基准（因为我们要的是最长距离的最小值），然后再把这些中立节点分入右半树，搞出相应的解，接下来我们比较刚才保存下来的基准，哪个小要哪种方案，这样我们就把最终的解搞出来了。
我觉得其实这种思路还可以推广，如果建立3个，4个乃至n个，我们也可以切割树求直径来搞。
然后切树是，我们可以通过把某个点“屏蔽”，来实现不会让dfs进入另一半子树的目的。
其实这个题还可以通过枚举大直径上的两点求出最优解来解决，思路也是比较清晰的。