题意
已知一个字符串 ![]() ,有
,有 ![]() 个询问需要你回答。
个询问需要你回答。
对于每个询问,有两种可能性:
- 1型:给你另外一个字符串
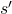 ,然后令
,然后令 。(即用新串更新当前的
。(即用新串更新当前的 )
) - 2型: 给你一个整数
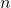 ,你要回答:可以构造多少种不同的长度为
,你要回答:可以构造多少种不同的长度为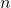 的字符串
的字符串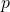 ,使得字符串
,使得字符串  是字符串
是字符串 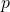 的一个子序列,只考虑英文小写字母.
的一个子序列,只考虑英文小写字母.
进一步解释:
- 子序列:假如有一个字符串
 ,我们去掉其中的一些字母(只能“去掉”,而不能交换字母的位置),得到另外一个串
,我们去掉其中的一些字母(只能“去掉”,而不能交换字母的位置),得到另外一个串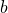 ,我们把
,我们把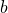 称为
称为 的子序列。
的子序列。 - 举个例子:
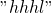 可以是
可以是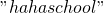 的子序列,
的子序列,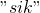 可以是
可以是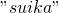 的子序列。
的子序列。
思路
首先,你需要注意到其实字符串![]() 的内容并不重要,影响答案的是字符串
的内容并不重要,影响答案的是字符串![]() 的长度。
的长度。
我们来考虑这样的一种思路:
假设我们构造的串是![]() ,
,![]() 是
是![]() 的子序列,我们设定:
的子序列,我们设定:![]() 在
在![]() 中的出现位置必须是字典序最小的。直白一点的说法:
中的出现位置必须是字典序最小的。直白一点的说法:![]() 是
是![]() 删除一些字母得到的,我们强制删除字母的时候,在连续相同的一段字母中,必须从右往左删。
删除一些字母得到的,我们强制删除字母的时候,在连续相同的一段字母中,必须从右往左删。
举两个例子方便理解这种想法:
![]() ,
,![]() 在
在![]() 中的对应位置必须是1、2、3、10(下标从1开始)。
中的对应位置必须是1、2、3、10(下标从1开始)。
![]() ,
,![]() 在
在![]() 中的对应位置必须是1、4、7、10(下标从1开始)。
中的对应位置必须是1、4、7、10(下标从1开始)。
有了这种想法我们就可以把s在固定的p中的对应位置关系唯一地确定下来。同时我们得到了这样的结论:
假设s的每一位在p中对应的位置为![]() ,字符串s的内容是
,字符串s的内容是![]() ,那么
,那么![]() 一定不会出现在p的第
一定不会出现在p的第![]() 位到
位到![]() 位,因为如果不这样的话,
位,因为如果不这样的话,![]() 在
在![]() 中的出现位置就不是“字典序最小”的了。
中的出现位置就不是“字典序最小”的了。
有了这个结论,我们就有了初步的想法,我们首先选择![]() 在
在![]() 中的出现位置,这个很简单,就是
中的出现位置,这个很简单,就是![]() (其中n是要构造的p的长度,|s|是s的长度),接下来,对于每种s在p中出现位置的分布,在第
(其中n是要构造的p的长度,|s|是s的长度),接下来,对于每种s在p中出现位置的分布,在第![]() 位之前的未填充空位,都可以填入25种字母(参见我们刚才得到的结论),在之后的空位,都可以任意填入26种字母。
位之前的未填充空位,都可以填入25种字母(参见我们刚才得到的结论),在之后的空位,都可以任意填入26种字母。
这样,如果我们枚举s在p中出现的最后位置![]() (下面用k表示),我们就可以算出答案,使用下面这个式子:
(下面用k表示),我们就可以算出答案,使用下面这个式子:
![]()
很显然如果直接拿这个式子出答案是![]() 的,不满足时间限制,我们要想些办法。
的,不满足时间限制,我们要想些办法。
观察一下上面的式子我们可以发现,可以提出![]() 这一项,这样对于相同的
这一项,这样对于相同的![]() ,不同的n的询问,我们只需要做一次
,不同的n的询问,我们只需要做一次![]() 的计算就可以全数回答。这提醒我们离线处理询问:把所有询问按照|s|为第一基准,n 为第二基准进行排序,依序处理,再按出现顺序排序,依序输出。
的计算就可以全数回答。这提醒我们离线处理询问:把所有询问按照|s|为第一基准,n 为第二基准进行排序,依序处理,再按出现顺序排序,依序输出。
这样做是可行的,因为![]() 最多有
最多有![]() 种(考虑极端情况:
种(考虑极端情况:![]() ,
,![]() ,
,![]() ,…,根据等差数列求和公式,项数最多只能到
,…,根据等差数列求和公式,项数最多只能到![]() ),对于每种不同的
),对于每种不同的![]() 都要做一个
都要做一个![]() 的处理,所以总复杂度为
的处理,所以总复杂度为![]() ,符合题目限制。
,符合题目限制。
至此本题圆满解决。
实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 |
#define REP(i,t) for(int i = 0;i < t; i++) #define REP_1(i,t) for(int i = 1;i <= t; i++) #define CASE_LOOP int ___;scanf(" %d",&___);for(int __ = 1; __ <= ___; __++) #define FOR_EDGE(i,u) for (int i = head[u]; i; i = nxt[i]) #define ADHOC_CIN(typ,name) typ name;cin >> name; using namespace std; typedef long long LL; int n; string cur; const int MAXN = 100005, MODER = 1000000007; LL fac[MAXN],fac_inv[MAXN]; LL fac26[MAXN],fac25[MAXN]; LL fac26_inv[MAXN],fac25_inv[MAXN]; LL get_mod(LL a){ if(a >= MODER || a < 0) a %= MODER; if(a < 0) a += MODER; return a; } LL mul_mod(LL a,LL b){ return get_mod(get_mod(a)*get_mod(b)); } LL pow_mod(LL a,LL p){ LL ret = 1; while (p) { if(p&1) ret = mul_mod(ret, a); a = mul_mod(a, a); p >>= 1; } return ret; } LL sum_mod(LL a,LL b){ return get_mod(get_mod(a) + get_mod(b)); } LL inv_mod(LL a){ return pow_mod(a, MODER-2); } void prep(){ fac[0] = fac_inv[0] = fac26[0] = fac25[0] = fac26_inv[0] = fac25_inv[0] = 1; REP_1(i, MAXN-1){ fac[i] = mul_mod(fac[i-1], i); fac_inv[i] = mul_mod(fac_inv[i-1], inv_mod(i)); fac26[i] = mul_mod(fac26[i-1], 26); fac25[i] = mul_mod(fac25[i-1], 25); fac26_inv[i] = mul_mod(fac26_inv[i-1], inv_mod(26)); fac25_inv[i] = mul_mod(fac25_inv[i-1], inv_mod(25)); } } LL C(LL n,LL r){ return mul_mod(fac[n], mul_mod(fac_inv[r], fac_inv[n-r])); } struct Query{ int id,len,qrn; LL res; } query[MAXN]; bool cmp_qrn(const Query &a,const Query &b){ if(a.qrn == b.qrn) return a.len < b.len; return a.qrn < b.qrn; } bool cmp_id(const Query &a,const Query &b){ return a.id < b.id; } int tot = 0; void solve(){ sort(query, query+tot, cmp_qrn); int cqrn = 0,ccur = 0; LL cval = 0; REP(i,tot){ if(query[i].len < query[i].qrn){ query[i].res = 0; continue; } if(query[i].qrn != cqrn){ ccur = cqrn = query[i].qrn; ccur--; cval = 0; } while(ccur < query[i].len){ ccur++; cval = sum_mod(cval, mul_mod(mul_mod(mul_mod(fac25[ccur], fac25_inv[cqrn]), fac26_inv[ccur]), C(ccur-1,cqrn-1))); } query[i].res = mul_mod(cval, fac26[query[i].len]); } sort(query, query+tot, cmp_id); REP(i, tot){ cout << query[i].res << endl; } } int main(int argc, const char * argv[]){ prep(); cin >> n >> cur; REP_1(i, n){ ADHOC_CIN(int, op); if(op == 1){ cin >> cur; }else{ ADHOC_CIN(int, a); query[tot] = {tot++,a,(int)cur.size(),0}; } } solve(); return 0; } |

![Rendered by QuickLaTeX.com al[h][w] =\sum \left\{\begin{matrix} {hf[1][w] \cdot (2\times hf[h-1][w-1] + 3\times hf[h-1][w-2] + 4\times hf[h-1][w-3] + ... + w\times hf[h-1][1])} \\ {hf[2][w] \cdot (2\times hf[h-2][w-1] + 3\times hf[h-2][w-2] + 4\times hf[h-2][w-3] + ... + w\times hf[h-2][1])} \\ {hf[3][w] \cdot (2\times hf[h-3][w-1] + 3\times hf[h-3][w-2] + 4\times hf[h-3][w-3] + ... + w\times hf[h-3][1])} \\ ... \\ {hf[h][w] \cdot (2\times hf[0][w-1] + 3\times hf[0][w-2] + 4\times hf[0][w-3] + ... + w\times hf[0][1])} \end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-c7e6d3390c11f69f46ca271b4c0859bd_l3.png)
![Rendered by QuickLaTeX.com al[h][w] = \sum \left\{\begin{matrix} hf[1][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[h-1][w-k] \\ hf[2][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[h-2][w-k] \\ hf[3][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[h-3][w-k] \\ ... \\ hf[h][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[0][w-k] \end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-cb751eded0c7e38d9a7452d89f308a35_l3.png)
![Rendered by QuickLaTeX.com dw[w] = \sum \left\{\begin{matrix} N\cdot al[1][w] \\ (N-1)\cdot al[2][w] \\ (N-2)\cdot al[3][w] \\ ... \\ 1 \cdot al[N][w] \end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-860e88577713d366e9a2e2cca7bdcb11_l3.png)
![Rendered by QuickLaTeX.com dw[w] = \sum \left\{\begin{matrix} N\times hf[1][w]\cdot rc[0][w] \\ (N-1)\times (hf[1][w]\cdot rc[1][w] + hf[2][w]\cdot rc[0][w]) \\ (N-2)\times (hf[1][w]\cdot rc[2][w] + hf[2][w]\cdot rc[1][w] + hf[3][w]\cdot rc[0][w]) \\ ... \\ 1\times (hf[1][w]\cdot rc[N-1][w] + hf[2][w]\cdot rc[N-2][w] + ... + hf[N][w]\cdot rc[0][w]) \end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-da7f01c212dea7f5d13313685f454a75_l3.png)
![Rendered by QuickLaTeX.com dw[w] = \sum \left\{\begin{matrix} hf[1][w]\times (N\cdot rc[0][w] + (N-1)\cdot rc[1][w] + (N-2)\cdot rc[2][w] + ... + 1\cdot rc[N-1][w]) \\ hf[2][w]\times ((N-1)\cdot rc[0][w] + (N-2)\cdot rc[1][w] + (N-3)\cdot rc[2][w] + ... + 1\cdot rc[N-2][w]) \\ hf[3][w]\times ((N-2)\cdot rc[0][w] + (N-3)\cdot rc[1][w] + (N-4)\cdot rc[2][w] + ... + 1\cdot rc[N-3][w]) \\ ... \\ hf[N][w] \times 1 \cdot rc[0][w] \end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-5582fffb95dead1ed52cdc683e471d67_l3.png)