最短路教程

February 16, 20172017-02-16hahaschoolLeave a comment

单源最短路

给出一个图 $G$ ，在图中选一个起点 $S$ ，我们要求出从起点到图上各点的最短路径，这就是单源最短路问题 (Single Source Shortest Path, SSSP)。

问题分析

无环性

最短路是NPC问题，但当保证了图中不存在负环时，化为P问题。
考虑如果有负环，就可以一直在负环上走，永远也不会到达最短。
最短路是指从起点到终点的路径，可能有多条，也可能不存在（起点和终点不联通？在起点到终点的路径上可能出现负环？）
最长路可以用最短路解决。
边权取负值，注意不可以有正环。
最短路不可能有环。
如果有正环，这个正环的一半完全可以不走。
如果有负环，可以不停在负环上走，永远取不到最短路。

最短路没有环

传递的最优性

若最短路 $u \rightarrow v$ 经过中间点 $w$ ，则 $u \rightarrow w$ 和 $w \rightarrow v$ 的路径分别是 $u$ 到 $w$ 和 $w$ 到 $v$ 的最短路。

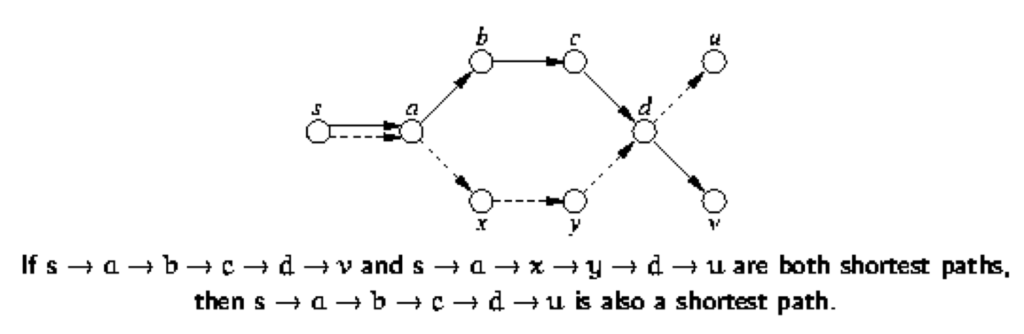
这是最短路最重要的性质，也是各种主流最短路算法的中心思想。

我们以下面图为例来进行解说，假设0号点为指定的起点：

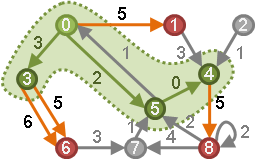
图中绿色的部分是我们目前已经“确认”了的区域，绿色的边就是我们找出的最短路，其他颜色的点都是我们没有找出最短路的点，我们可以发现在已确认区域内部，上面的传递性当然是成立的。

再考虑图中红色的部分，这些都是从绿色区域可以直接到达的，也就意味着一定存在一条路径，前面若干条边都是绿色的，最后一条边是红色的，而且这条路径是从起点到红色的店的最短路（当然，在确定了这条最短路之后，这个红色的点和红色的边会被设定为绿色，这个点的其他入边会变为灰色）。
这种性质提示我们可以记录从起点到已经确认的点的最短路，也就是说利用动态规划的思想。

同时我们也可以提出下面的两种贪心想法：

如果一个红色的点的所有入边都已经变红，只要选取里面最短的那个红边纳入最短路，就可以得到这个点对应的最短路（最短连最短一定最短）。
如果没有任何一个红点的所有入边都变红，那么我们可以试算每个红点经由红边得到的最短路，挑选里面最短的那个纳入绿色区域（因为这个时候这个点已经不可能取到更短的路径了）。

根据最优性的传递性，这两种贪心的想法都是合理的。主流的最短路算法都是基于动态规划思想和贪心思想的。

最短路树/最短路DAG

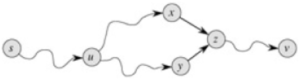
前面提到了最短路的无环性和传递性，假设每个点对应的最短路的解是唯一的，我们可以轻松发现，把所有点的最短路对应边在图上染出来，同所有的点一起正好形成一棵树。

如果考虑多解，就会形成一个DAG。

算法

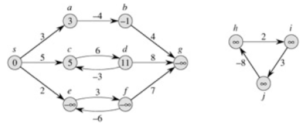
下面将会介绍几种主流的单源最短路算法及其实现，依然以此图举例：

在开始之前，我们要介绍一个术语“松弛(Relax)”，松弛操作可以表示为：

if(dis[v] > dis[u] + len[i]) {
    dis[v] = dis[u] + len[i];
    prv[v] = u;
}

if(dis[v] > dis[u] + len[i]) {

dis[v] = dis[u] + len[i];

prv[v] = u;

}

其中dis是从起点到某个点的距离，len是边的长度，u是一个绿色点，v是一个红色点，prv表示某个点在最短路上的前趋。也就是说松弛操作实际上就是试算红色点最短路的过程。

Bellman-Ford

Bellman-Ford 算法可以概括为：不停进行迭代，每次迭代尝试松弛所有边，迭代最多进行 $V-1$ 次( $V$ 是图的点数)，如果一次迭代中没有进行任何成功的松弛，算法可以立即终止，算法复杂度为 $O(VE)$ （E是图的边数）。实现如下：

//    n       : 点数
//    m       : 边数
//    dis[x]  : 从起点到x的最短路长度
//    from[i] : i号边从哪个点开始
//    ed[i]   : i号边到哪个点结束
//    len[i]  : i号边长度
//    prv[x]  : x的最短路前趋
    //一开始，所有点的dis都设为无穷大，起点设为0
    for(int i = 1;i <= n;i++){
        dis[i] = INF;
    }
    dis[s] = 0;
    //最多进行n-1次迭代
    for(int i = 1;i <= n-1; i++){
        bool relaxed = false;
        for(int j = 1;j <= m; j++){
            //对每条边都尝试一次松弛操作
            int u = from[j], v = ed[j];
            if(dis[v] > dis[u] + len[j]){
                dis[v] = dis[u] + len[j];
                prv[v] = u;
                relaxed = true;
            }
        }
        //如果没有一次成功的松弛，算法可以提前退出
        if(!relaxed) break;
    }

// n : 点数

// m : 边数

// dis[x] : 从起点到x的最短路长度

// from[i] : i号边从哪个点开始

// ed[i] : i号边到哪个点结束

// len[i] : i号边长度

// prv[x] : x的最短路前趋

//一开始，所有点的dis都设为无穷大，起点设为0

for(int i = 1;i <= n;i++){

dis[i] = INF;

}

dis[s] = 0;

//最多进行n-1次迭代

for(int i = 1;i <= n-1; i++){

bool relaxed = false;

for(int j = 1;j <= m; j++){

//对每条边都尝试一次松弛操作

int u = from[j], v = ed[j];

if(dis[v] > dis[u] + len[j]){

dis[v] = dis[u] + len[j];

prv[v] = u;

relaxed = true;

}

//如果没有一次成功的松弛，算法可以提前退出

if(!relaxed) break;

}

为什么这种算法是合理的呢？联想我们提到的最短路的性质：

所有的最短路形成树，根据树的性质，N个点的树有N-1条边。
基于两个贪心的想法，如果我们每一轮迭代都松弛每个边，每一轮都可以确定一个红点成为旅店，一定至少往最短路树中增加一条边。
这样，我们至多经过N-1次迭代可以得到最短路。

如果图里有负环，会发生什么呢？我们知道经过N-1次迭代就可以确认所有点的最短路了，也就是说第N次迭代将会没有成功的松弛。但是如果有负环，松弛过程将不断尝试在负环中回环，也就是说第N次迭代中将会出现成功松弛。我们可以利用这个特性来判断图中是否有负环。

SPFA

Shortest Path Faster Algorithm实际上是Bellman-Ford的队列实现。我们注意到在上面的迭代实现中，我们每一次都访问了许多绿色边和灰色边，而这些边的松弛操作实际上都是没有用的，如果我们使用队列实现，每一次只松弛红色边，算法的效率就会有所提高。SPFA的代码实现如下：

//n:点数
//m:边数
//dis[x]:起点到x的最短路距离
//inque[x]:x点是否在队列里
//prv[x]:x点的最短路前趋
//head[],nxt[],from[],ed[]:参见邻接表

queue<int> que;
//初始化dis数组和inque数组
for(int i = 1;i <= n;i++){
    dis[i] = INF;
    inque[i] = false;
}
dis[s] = 0;
que.push(s);
inque[s] = true;
while(!que.empty()){
    int u = que.front();
    que.pop();
    inque[u] = false;
    for(int i = head[u];i;i = nxt[i]){
        if(dis[v] > dis[u] + len[i]){
            dis[v] = dis[u] + len[i];
            prv[i] = u;
            if(!inque[v]){
                que.push(v);
                inque[v] = true;
            }
        }
    }
}

//n:点数

//m:边数

//dis[x]:起点到x的最短路距离

//inque[x]:x点是否在队列里

//prv[x]:x点的最短路前趋

//head[],nxt[],from[],ed[]:参见邻接表

queue<int> que;

//初始化dis数组和inque数组

for(int i = 1;i <= n;i++){

dis[i] = INF;

inque[i] = false;

}

dis[s] = 0;

que.push(s);

inque[s] = true;

while(!que.empty()){

int u = que.front();

que.pop();

inque[u] = false;

for(int i = head[u];i;i = nxt[i]){

if(dis[v] > dis[u] + len[i]){

dis[v] = dis[u] + len[i];

prv[i] = u;

if(!inque[v]){

que.push(v);

inque[v] = true;

}

SPFA的复杂度与Bellman-Ford相同，都是 $O(VE)$ ，然而在实际应用中，SPFA很少会达到这么高时间，在一些情况中，SPFA的效率甚至比Dijkstra高。

Dijkstra

Dijkstra算法适用于所有的边权都为正的图，算法的语言表述如下：

初始化访问标记数组vis[]为全false，vis[x]表示x是否被访问过
初始化距离数组dis[]为全INF，dis[起点s]为0，dis[x]表示起点到s的距离
执行n次下述过程（n为图的点数）：
1. 在所有vis为false的点中挑一个对应的dis值最小的出来（如果有多个就随便选一个），令其为u
2. 令vis[u]=true
3. 对于所有u出发的边，进行一次松弛操作

可以发现，在Dijkstra算法中，一个点只要被访问，就会变成绿色点，也就是这个点对应的最短路被确认。联想我们上面提到过的传递性质里面的贪心思想，不难说明这种方法的合理性。假设一个点t在被访问的时候并没有取到最短路，那么必然存在另外一条更短路径能够到达t点，因为我们每一次挑选dis最小的点访问，那么这条更短路径中与t邻接的那个点必然会被先行访问，所以不存在这种不合理的情况。

那么，为什么Dijkstra不适用于带有负权边也可以得到解释，如果没有负权边，最短路径上面的dis值可以保证单调，然而引入负权边之后这种单调性就消失了，我们之前的贪心策略也就不合理了。

Dijkstra的实现难点主要在“挑选已访问点中dis最小的那个”这一步上，这里是Dijkstra性能的瓶颈，这一步通常使用堆结构来实现。C++ STL中自带的优先队列由于无法进行堆内值的变更操作，所以实现出来的复杂度并不稳定（因为部分点会重复入队），而且可能需要使用仿函数技术进行运算符重载，一个如此实现的例子如下：

//n:点数
//m:边数
//dis[x]:起点到x的最短路距离
//vis[x]:x点是否在访问过
//prv[x]:x点的最短路前趋
//head[],nxt[],from[],ed[]:参见邻接表

struct Node{
    int id,dis;
    bool operator () (const Node &a, const Node &b){
        return a.dis < b.dis;
    }
};

priority_queue<Node, vector<Node>, greater<Node> > que;
for(int i = 1;i <= n;i++){
    dis[i] = INF;
    vis[i] = false;
}
dis[s] = 0;
que.push(s);
while(!que.empty()){
    int u = que.top().id;
    que.pop();
    vis[u] = true;
    for(int i = head[u];i;i = nxt[i]){
        int v = ed[i];
        if(!vis[v] && dis[v] > dis[u] + len[i]){
            dis[v] = dis[u] + len[i];
            prv[i] = u;
            que.push({v,dis[v]});
        }
    }
}

//n:点数

//m:边数

//dis[x]:起点到x的最短路距离

//vis[x]:x点是否在访问过

//prv[x]:x点的最短路前趋

//head[],nxt[],from[],ed[]:参见邻接表

struct Node{

int id,dis;

bool operator () (const Node &a, const Node &b){

return a.dis < b.dis;

}

};

priority_queue<Node, vector<Node>, greater<Node> > que;

for(int i = 1;i <= n;i++){

dis[i] = INF;

vis[i] = false;

}

dis[s] = 0;

que.push(s);

while(!que.empty()){

int u = que.top().id;

que.pop();

vis[u] = true;

for(int i = head[u];i;i = nxt[i]){

int v = ed[i];

if(!vis[v] && dis[v] > dis[u] + len[i]){

dis[v] = dis[u] + len[i];

prv[i] = u;

que.push({v,dis[v]});

}

可以发现在实现的思路上实际上与SPFA并无太大区别，其实我们也可以把SPFA中的普通队列换成优先队列，可以有一定的启发式作用。

要真正地实现Dijkstra，除了自己手写堆之外，还可以考虑使用pd_ds扩展库，p b_ds中提供了可以调整堆内值的优先队列，但是pb_ds并不一定在所有环境中提供，有一定风险。

Gabow

这是一种与前面若干种方法截然不同的最短路算法，使用Scaling Method，这不是本文在当前版本要讨论的内容。

应用

[…待更]

多源最短路

问题概述

在单源最短路的基础上，多源最短路问题要求快速求出图中任意点对之间的最短路。

算法

除了运行N次单源最短路之外，多源最短路问题还有一种实现起来异常简单的Floyd-Warshall算法，其本质是动态规划。

for(int k = 1;i <= n; i++){
    for(int i = 1;j <= n; j++){
        for(int j = 1; k <= n; k++){
            dis[i][j] = min(dis[i][j],dis[i][k] + dis[k][j]);
        }
    }
}

for(int k = 1;i <= n; i++){

for(int i = 1;j <= n; j++){

for(int j = 1; k <= n; k++){

dis[i][j] = min(dis[i][j],dis[i][k] + dis[k][j]);

}

其中dis[i][j]是邻接矩阵，如果i->j邻接，则值为边权，否则为无穷大。在实现过程中，注意三个循环的顺序为kij并非ijk，这是为了利用CPU的缓存优化，尽量不跳行读取，这种优化可以大大提高程序运行效率。

应用

[…待更]

总结

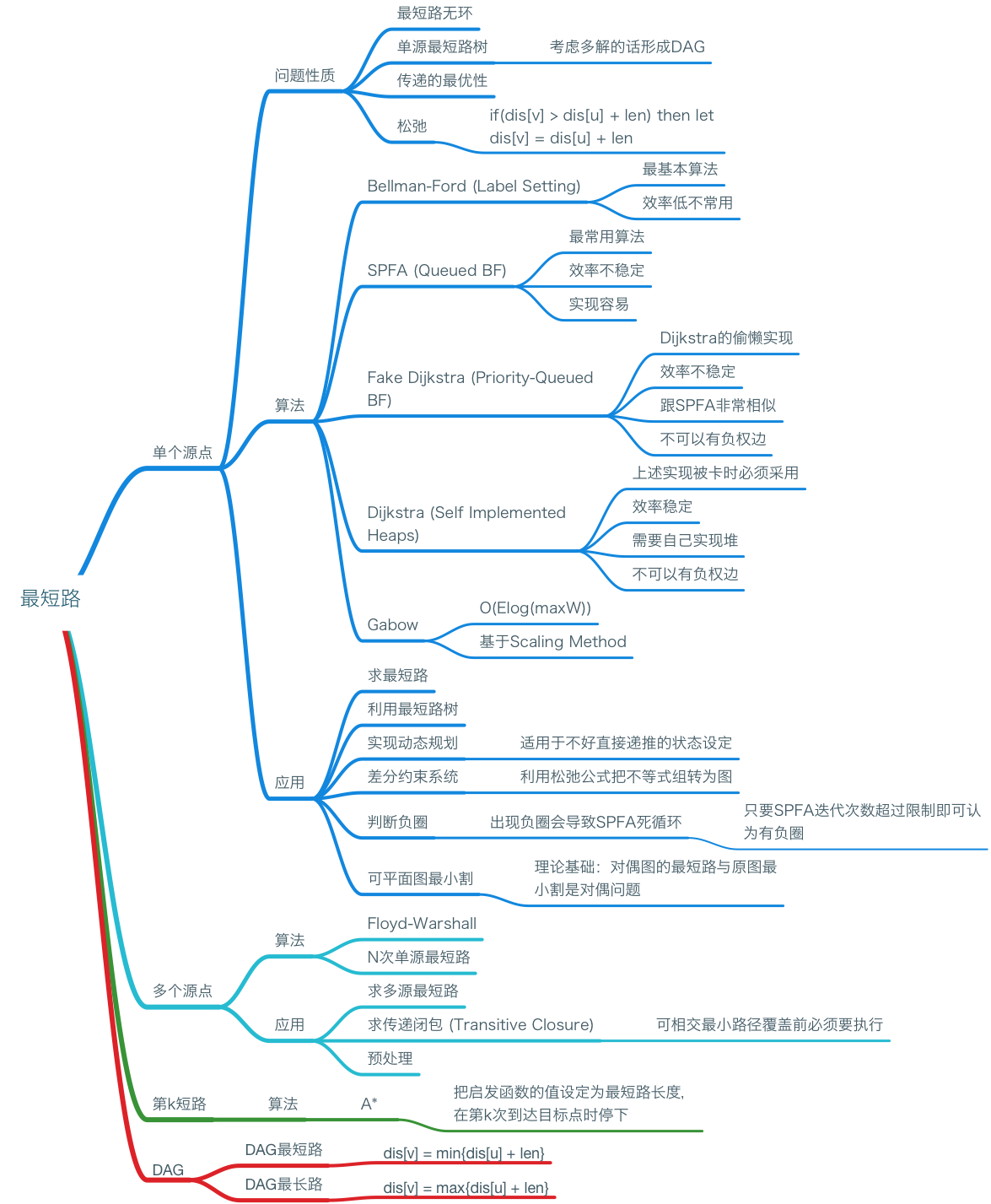
下面这张简单的思维导图大略的列出了最短路相关的部分考点。

最短路相关知识的思维导图

参考

Codeforces 666C Codewords

October 12, 20162016-10-12hahaschoolLeave a comment

题意

已知一个字符串 $s$ ，有 $m$ 个询问需要你回答。

对于每个询问，有两种可能性：

1型：给你另外一个字符串 $s'$ ，然后令 $s = s'$ 。（即用新串更新当前的 $s$ ）
2型：给你一个整数 $n$ ，你要回答：可以构造多少种不同的长度为 $n$ 的字符串 $p$ ，使得字符串 $s$ 是字符串 $p$ 的一个子序列，只考虑英文小写字母.

进一步解释：

子序列：假如有一个字符串 $a$ ，我们去掉其中的一些字母（只能“去掉”，而不能交换字母的位置），得到另外一个串 $b$ ，我们把 $b$ 称为 $a$ 的子序列。
举个例子： $"hhhl"$ 可以是 $"hahaschool"$ 的子序列， $"sik"$ 可以是 $"suika"$ 的子序列。

思路

首先，你需要注意到其实字符串 $s$ 的内容并不重要，影响答案的是字符串 $s$ 的长度。

我们来考虑这样的一种思路：

假设我们构造的串是 $p$ ， $s$ 是 $p$ 的子序列，我们设定： $s$ 在 $p$ 中的出现位置必须是字典序最小的。直白一点的说法： $s$ 是 $p$ 删除一些字母得到的，我们强制删除字母的时候，在连续相同的一段字母中，必须从右往左删。

举两个例子方便理解这种想法：

$s = "hahl" p = "hahaschool"$ ， $"hahl"$ 在 $"hahaschool"$ 中的对应位置必须是1、2、3、10（下标从1开始）。

$s = "abad" p = "aaabbbaaaddd"$ ， $"abad"$ 在 $"aaabbbaaaddd"$ 中的对应位置必须是1、4、7、10（下标从1开始）。

有了这种想法我们就可以把s在固定的p中的对应位置关系唯一地确定下来。同时我们得到了这样的结论：

假设s的每一位在p中对应的位置为 $p_i$ ，字符串s的内容是 $s_i$ ，那么 $s_{k+1}$ 一定不会出现在p的第 $p_k$ 位到 $p_{k+1}-1$ 位，因为如果不这样的话， $s$ 在 $p$ 中的出现位置就不是“字典序最小”的了。

有了这个结论，我们就有了初步的想法，我们首先选择 $s$ 在 $p$ 中的出现位置，这个很简单，就是 $\binom{n}{|s|}$ （其中n是要构造的p的长度，|s|是s的长度），接下来，对于每种s在p中出现位置的分布，在第 $p_{|s|}$ 位之前的未填充空位，都可以填入25种字母（参见我们刚才得到的结论），在之后的空位，都可以任意填入26种字母。

这样，如果我们枚举s在p中出现的最后位置 $p_{|s|}$ （下面用k表示），我们就可以算出答案，使用下面这个式子：

$ans=\sum_{k=|s|}^{n}\binom{k-1}{|s|-1}25^{k-|s|}26^{n-k}$

很显然如果直接拿这个式子出答案是 $O(n^2)$ 的，不满足时间限制，我们要想些办法。

观察一下上面的式子我们可以发现，可以提出 $26^n$ 这一项，这样对于相同的 $|s|$ ，不同的n的询问，我们只需要做一次 $O(n)$ 的计算就可以全数回答。这提醒我们离线处理询问：把所有询问按照|s|为第一基准，n 为第二基准进行排序，依序处理，再按出现顺序排序，依序输出。

这样做是可行的，因为 $|s|$ 最多有 $\sqrt{n}$ 种（考虑极端情况： ${|s|}_1 = 1$ , ${|s|}_2 = 2$ , ${|s|}_3 = 3$ ,…，根据等差数列求和公式，项数最多只能到 $\sqrt{100000}$ ），对于每种不同的 $|s|$ 都要做一个 $O(n)$ 的处理，所以总复杂度为 $O(n\sqrt{n})$ ，符合题目限制。

至此本题圆满解决。

实现

#define REP(i,t) for(int i = 0;i < t; i++)
#define REP_1(i,t) for(int i = 1;i <= t; i++)
#define CASE_LOOP int ___;scanf(" %d",&___);for(int __ = 1; __ <= ___; __++)
#define FOR_EDGE(i,u) for (int i = head[u]; i; i = nxt[i])
#define ADHOC_CIN(typ,name) typ name;cin >> name;

using namespace std;

typedef long long LL;

int n;
string cur;

const int MAXN = 100005, MODER = 1000000007;
LL fac[MAXN],fac_inv[MAXN];
LL fac26[MAXN],fac25[MAXN];
LL fac26_inv[MAXN],fac25_inv[MAXN];
LL get_mod(LL a){
    if(a >= MODER || a < 0) a %= MODER;
    if(a < 0) a += MODER;
    return a;
}

LL mul_mod(LL a,LL b){
    return get_mod(get_mod(a)*get_mod(b));
}

LL pow_mod(LL a,LL p){
    LL ret = 1;
    while (p) {
        if(p&1) ret = mul_mod(ret, a);
        a = mul_mod(a, a);
        p >>= 1;
    }
    return ret;
}

LL sum_mod(LL a,LL b){
    return get_mod(get_mod(a) + get_mod(b));
}

LL inv_mod(LL a){
    return pow_mod(a, MODER-2);
}

void prep(){
    fac[0] = fac_inv[0] = fac26[0] = fac25[0] = fac26_inv[0] = fac25_inv[0] =  1;
    REP_1(i, MAXN-1){
        fac[i] = mul_mod(fac[i-1], i);
        fac_inv[i] = mul_mod(fac_inv[i-1], inv_mod(i));
        fac26[i] = mul_mod(fac26[i-1], 26);
        fac25[i] = mul_mod(fac25[i-1], 25);
        fac26_inv[i] = mul_mod(fac26_inv[i-1], inv_mod(26));
        fac25_inv[i] = mul_mod(fac25_inv[i-1], inv_mod(25));
    }
}

LL C(LL n,LL r){
    return mul_mod(fac[n], mul_mod(fac_inv[r], fac_inv[n-r]));
}

struct Query{
    int id,len,qrn;
    LL res;
} query[MAXN];

bool cmp_qrn(const Query &a,const Query &b){
    if(a.qrn == b.qrn) return a.len < b.len;
    return a.qrn < b.qrn;
}

bool cmp_id(const Query &a,const Query &b){
    return a.id < b.id;
}

int tot = 0;

void solve(){
    sort(query, query+tot, cmp_qrn);
    int cqrn = 0,ccur = 0;
    LL cval = 0;
    REP(i,tot){
        if(query[i].len < query[i].qrn){
            query[i].res = 0;
            continue;
        }
        if(query[i].qrn != cqrn){
            ccur = cqrn = query[i].qrn;
            ccur--;
            cval = 0;
        }
        while(ccur < query[i].len){
            ccur++;
            cval = sum_mod(cval, mul_mod(mul_mod(mul_mod(fac25[ccur], fac25_inv[cqrn]), fac26_inv[ccur]), C(ccur-1,cqrn-1)));
        }
        query[i].res = mul_mod(cval, fac26[query[i].len]);
    }

    sort(query, query+tot, cmp_id);
    REP(i, tot){
        cout << query[i].res << endl;
    }
}

int main(int argc, const char * argv[]){
    prep();
    cin >> n >> cur;
    REP_1(i, n){
        ADHOC_CIN(int, op);
        if(op == 1){
            cin >> cur;
        }else{
            ADHOC_CIN(int, a);
            query[tot] = {tot++,a,(int)cur.size(),0};
        }
    }
    solve();
    return 0;
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

#define REP(i,t) for(int i = 0;i < t; i++)

#define REP_1(i,t) for(int i = 1;i <= t; i++)

#define CASE_LOOP int ___;scanf(" %d",&___);for(int __ = 1; __ <= ___; __++)

#define FOR_EDGE(i,u) for (int i = head[u]; i; i = nxt[i])

#define ADHOC_CIN(typ,name) typ name;cin >> name;

using namespace std;

typedef long long LL;

int n;

string cur;

const int MAXN = 100005, MODER = 1000000007;

LL fac[MAXN],fac_inv[MAXN];

LL fac26[MAXN],fac25[MAXN];

LL fac26_inv[MAXN],fac25_inv[MAXN];

LL get_mod(LL a){

if(a >= MODER || a < 0) a %= MODER;

if(a < 0) a += MODER;

return a;

}

LL mul_mod(LL a,LL b){

return get_mod(get_mod(a)*get_mod(b));

}

LL pow_mod(LL a,LL p){

LL ret = 1;

while (p) {

if(p&1) ret = mul_mod(ret, a);

a = mul_mod(a, a);

p >>= 1;

}

return ret;

}

LL sum_mod(LL a,LL b){

return get_mod(get_mod(a) + get_mod(b));

}

LL inv_mod(LL a){

return pow_mod(a, MODER-2);

}

void prep(){

fac[0] = fac_inv[0] = fac26[0] = fac25[0] = fac26_inv[0] = fac25_inv[0] = 1;

REP_1(i, MAXN-1){

fac[i] = mul_mod(fac[i-1], i);

fac_inv[i] = mul_mod(fac_inv[i-1], inv_mod(i));

fac26[i] = mul_mod(fac26[i-1], 26);

fac25[i] = mul_mod(fac25[i-1], 25);

fac26_inv[i] = mul_mod(fac26_inv[i-1], inv_mod(26));

fac25_inv[i] = mul_mod(fac25_inv[i-1], inv_mod(25));

}

LL C(LL n,LL r){

return mul_mod(fac[n], mul_mod(fac_inv[r], fac_inv[n-r]));

}

struct Query{

int id,len,qrn;

LL res;

} query[MAXN];

bool cmp_qrn(const Query &a,const Query &b){

if(a.qrn == b.qrn) return a.len < b.len;

return a.qrn < b.qrn;

}

bool cmp_id(const Query &a,const Query &b){

return a.id < b.id;

}

int tot = 0;

void solve(){

sort(query, query+tot, cmp_qrn);

int cqrn = 0,ccur = 0;

LL cval = 0;

REP(i,tot){

if(query[i].len < query[i].qrn){

query[i].res = 0;

continue;

}

if(query[i].qrn != cqrn){

ccur = cqrn = query[i].qrn;

ccur--;

cval = 0;

}

while(ccur < query[i].len){

ccur++;

cval = sum_mod(cval, mul_mod(mul_mod(mul_mod(fac25[ccur], fac25_inv[cqrn]), fac26_inv[ccur]), C(ccur-1,cqrn-1)));

}

query[i].res = mul_mod(cval, fac26[query[i].len]);

}

sort(query, query+tot, cmp_id);

REP(i, tot){

cout << query[i].res << endl;

}

int main(int argc, const char * argv[]){

prep();

cin >> n >> cur;

REP_1(i, n){

ADHOC_CIN(int, op);

if(op == 1){

cin >> cur;

}else{

ADHOC_CIN(int, a);

query[tot] = {tot++,a,(int)cur.size(),0};

}

solve();

return 0;

}

Codeforces 295D Greg and Caves

October 12, 20162018-04-07hahaschoolLeave a comment

题意

你有一个 $n*m$ 大小的棋盘， $n$ 行， $m$ 列，行号列号都从 $1$ 开始，行从上到下数到 $n$ ，列从左到右数到 $m$ ，棋盘的每一个格子可以是黑色或者白色。

当满足全部下述条件的时候，认为棋盘上出现了一个”Cave“：

存在一个线段 $[l,r] (1 <= l <= r <= n)$ ，使得 $l,l+1,l+2,...,r$ 这些行都有且仅有两个黑色格子，其他行不存在黑色格子。
存在一个行号，使得：
- 对于任意存在黑色格子的行 $r$ ，把这行的黑色格子对应的列号和黑色格子之间的列号加入一个集合，称之为 $S(r)$ 。
- 任取t及t之上的两个有黑色格子的行，令上方的行为 $u$ ，下方的行 $d$ ，则 $S(u)$ 是 $S(d)$ 的子集。
- 任取 $t$ 及 $t$ 之下的两个有黑色格子的行，令上方的行为 $u$ ，下方的行为 $d$ ，则 $S(d)$ 是 $S(u)$ 的子集。

你要输出有多少染色的方案，使得棋盘出现一个“Cave”，答案模 $1000000007$ 。

思路

翻译一下题意，就是让我们找一种染色方案，让棋盘上出现下面这样的图案（下图中 $n = m = 5 ,l = 3, r = 15, t = 8$ ）。

295D

可以发现，这个图案可以以t行为界分拆为上下两个部分，不妨令 $hf[h][w]$ 表示得到高度为h的，底部两个黑块宽度必须为w的，每一行都有黑块的，半个图案的染色方案数。

我们可以很容易发现如下的递推关系：

$hf[h][w] = {hf[h-1][w] + 2\times hf[h-1][w-1] + 3\times hf[h-1][w-2] +4\times hf[h-1][w-3] + ... + w\times hf[h-1][1]}$

即：

$hf[h][w] = \sum_{k=1}^{w} k\cdot hf[h-1][w+1-k]$

考虑同一高度的相邻两项之差：

$hf[h][w] - hf[h][w-1] = \sum_{k=1}^{w} hf[h-1][k]$

这样，我们一行行地计算 $hf$ 的值，一边维护每一行的前缀和，一边算下一项，这样可以用 $O(n^2)$ 的时间完成预处理。

接下来我们考虑如何把两个一半的图案合成一个，我们令 $al[h][w]$ 表示得到高度为 $h$ ，最宽处宽度为 $w$ ，每一行都有黑块的图案的染色方案数，我们有：

$al[h][w] =\sum \left\{\begin{matrix} {hf[1][w] \cdot (2\times hf[h-1][w-1] + 3\times hf[h-1][w-2] + 4\times hf[h-1][w-3] + ... + w\times hf[h-1][1])} \\ {hf[2][w] \cdot (2\times hf[h-2][w-1] + 3\times hf[h-2][w-2] + 4\times hf[h-2][w-3] + ... + w\times hf[h-2][1])} \\ {hf[3][w] \cdot (2\times hf[h-3][w-1] + 3\times hf[h-3][w-2] + 4\times hf[h-3][w-3] + ... + w\times hf[h-3][1])} \\ ... \\ {hf[h][w] \cdot (2\times hf[0][w-1] + 3\times hf[0][w-2] + 4\times hf[0][w-3] + ... + w\times hf[0][1])} \end{matrix}\right.$

即：

$al[h][w] = \sum \left\{\begin{matrix} hf[1][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[h-1][w-k] \\ hf[2][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[h-2][w-k] \\ hf[3][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[h-3][w-k] \\ ... \\ hf[h][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[0][w-k] \end{matrix}\right.$

为了让式子更简洁，我们令 $rc[h][w] = \sum_{k=1}^{w-1} (k+1)\cdot hf[h][w-k]$ ，这样的话，我们就有：

$al[h][w] = \sum_{k=1}^{h} hf[k][w]\cdot rc[h-k][w]$

很明显这个式子是一个卷积，如果我们可以预处理出 $rc$ 的值，就可以使用FFT进行快速运算。我们发现 $rc$ 的递推关系和 $hf$ 的递推关系非常相似，我们依然考虑同行相邻两项的差值：

$rc[h][w] - rc[h][w-1] = hf[h][w-1] + \sum_{k=1}^{w-1} hf[h][w-k]$

这样我们依然采用一边计算一边维护前缀和的方法，可以在 $O(n^2)$ 的时间完成 $rc$ 的预处理。

预处理好 $rc$ 之后，就是计算卷积了，因为题目要求模 $1000000007$ ，我们需要采用NTT+CRT的方式实现任意模空间下的卷积（具体实现原理不是我们的讨论范围），这样的话，在最恶劣情况，我们需要做18000次4096点NTT，单次NTT耗时几毫秒，超时无法避免，我们只能考虑进一步优化。

我们继续考虑，令 $dw[w]$ 表示最宽处宽度为 $w$ ，高度范围在 $1 \sim N$ 的图案，有多少方案可以作成，那么我们有：

$dw[w] = \sum \left\{\begin{matrix} N\cdot al[1][w] \\ (N-1)\cdot al[2][w] \\ (N-2)\cdot al[3][w] \\ ... \\ 1 \cdot al[N][w] \end{matrix}\right.$

把 $al$ 打开，就有：

$dw[w] = \sum \left\{\begin{matrix} N\times hf[1][w]\cdot rc[0][w] \\ (N-1)\times (hf[1][w]\cdot rc[1][w] + hf[2][w]\cdot rc[0][w]) \\ (N-2)\times (hf[1][w]\cdot rc[2][w] + hf[2][w]\cdot rc[1][w] + hf[3][w]\cdot rc[0][w]) \\ ... \\ 1\times (hf[1][w]\cdot rc[N-1][w] + hf[2][w]\cdot rc[N-2][w] + ... + hf[N][w]\cdot rc[0][w]) \end{matrix}\right.$

我们把 $dw[w]$ 重新整理一下：

$dw[w] = \sum \left\{\begin{matrix} hf[1][w]\times (N\cdot rc[0][w] + (N-1)\cdot rc[1][w] + (N-2)\cdot rc[2][w] + ... + 1\cdot rc[N-1][w]) \\ hf[2][w]\times ((N-1)\cdot rc[0][w] + (N-2)\cdot rc[1][w] + (N-3)\cdot rc[2][w] + ... + 1\cdot rc[N-2][w]) \\ hf[3][w]\times ((N-2)\cdot rc[0][w] + (N-3)\cdot rc[1][w] + (N-4)\cdot rc[2][w] + ... + 1\cdot rc[N-3][w]) \\ ... \\ hf[N][w] \times 1 \cdot rc[0][w] \end{matrix}\right.$

如果比较敏感的话应该已经发现突破口了，我们再整理一下：

$dw[w] = \sum_{i=1}^{N}hf[i][w]\sum_{j=0}^{N-i}((N-i-j+1)\cdot rc[j][w])$

还没看出来？再令 $tr[i][w] = \sum_{j=0}^{N-i}((N-i-j+1)\cdot rc[j][w])$ ，这样：

$dw[w] = \sum_{i=1}^{N}hf[i][w]\cdot tr[i][w]$

而且我们还可以发现 $hf, rc, tr$ 它们的递推关系都是差不多的，也就是说对于 $tr$ 我们继续采用考虑相邻两项差的策略：

$tr[i][w] - tr[i-1][w] = \sum_{k=0}^{N-i} rc[k][w]$

这样我们可以用 $O(n^2)$ 的时间把 $tr$ 搞定，这样的话，计算全部的 $dw$ 的值也是 $O(n^2)$ 时间了。

计算好表示定宽度不定高度的图案数的 $dw$ 之后，接下来我们放宽到不定宽度不定高度的图案数，也就是答案，我们有：

$ans = \sum_{w=2}^{M}(M-w+1)\cdot dw[w]$

这样我们绕了一大圈终于把答案算出来了，总复杂度 $O(n^2)$ ，本题至此解决。

实现

NTT+CRT做法

注意这份代码因为常数过大无法通过，但是答案是正确的。

//NTT Version
//Warning:Severely Exceeds TL(14s,TL2s),although O(n^2logn)

#define REP(i,t) for(int i = 0;i < t; i++)
#define REP_1(i,t) for(int i = 1;i <= t; i++)
#define CASE_LOOP int ___;scanf(" %d",&___);for(int __ = 1; __ <= ___; __++)
#define FOR_EDGE(i,u) for (int i = head[u]; i; i = nxt[i])
#define ADHOC_CIN(typ,name) typ name;cin >> name;
#define ADHOC_SCANINT(name) int name;scanf(" %d",&name);


using namespace std;

typedef long long LL;
typedef long double LD;

#define USUAL_MODANY
#ifdef USUAL_MODANY
inline LL getmod(LL a,LL m){if(a<0||a>=m)a%=m;if(a<0)a+=m;return a;}
inline LL summod(LL a,LL b,LL m){return getmod(getmod(a,m)+getmod(b,m),m);}
inline LL mulmod(LL a,LL b,LL m){return getmod(getmod(a,m)*getmod(b,m),m);}
inline LL powmod(LL a,LL p,LL m){LL ret=1;while(p){if(p&1)ret=mulmod(ret,a,m);a=mulmod(a,a,m);p>>=1;}return ret;}
inline LL invmod(LL a,LL m){return powmod(a,m-2,m);}
#endif

#define NTT_MOD_ANY
#ifdef NTT_MOD_ANY
// 多项式乘法 系数对MOD=1000000007取模， 常数巨大，慎用
// 只要选的K个素数乘积大于MOD*MOD*N,理论上MOD可以任取。
#define MOD 1000000007
#define K 3
//用于CRT的三个模空间
const int m[K] = {1004535809, 998244353, 104857601};
//479*2^21+1,7*17*2^23+1,25*2^22+1
//m[0] > m[1] > m[2]
#define G 3
//上述三个素数的原根

const int MAXN = 4444;

inline int qpow(int x, int k, int P) {
    int ret = 1;
    while(k) {
        if(k & 1) ret = 1LL * ret * x % P;
        k >>= 1;
        x = 1LL * x * x % P;
    }
    return ret;
}

struct _NTT {
    //wn:旋转分量 P:模空间(P-1是2的幂)
    int wn[25], P;
    //init(_P)用给出的模空间_P构建旋转分量
    void init(int _P) {
        P = _P;
        for(int i = 1; i <= 21; ++i) {
            int t = 1 << i;
            wn[i] = qpow(G, (P - 1) / t, P);
        }
    }

    //RADAR编码
    //FFT与IFFT之前的反转变换
    //位置i和(i的二进制反转)位置互换
    //len需要是2的幂
    void change(int *y, int len) {
        for(int i = 1, j = len / 2; i < len - 1; ++i) {
            if(i < j) swap(y[i], y[j]);
            int k = len / 2;
            while(j >= k) {
                j -= k;
                k /= 2;
            }
            j += k;
        }
    }

    //NTT主过程，y是等待变换的数组，下标从0开始，长度为len
    //len是2的幂
    //on=1的话NTT on=-1的话INTT
    void NTT(int *y, int len, int on) {
        change(y, len);
        int id = 0;

        for(int h = 2; h <= len; h <<= 1) {
            ++id;
            for(int j = 0; j < len; j += h) {
                int w = 1;
                for(int k = j; k < j + h / 2; ++k) {
                    int u = y[k];
                    int t = 1LL * y[k+h/2] * w % P;
                    y[k] = u + t;
                    if(y[k] >= P) y[k] -= P;
                    y[k+h/2] = u - t + P;
                    if(y[k+h/2] >= P) y[k+h/2] -= P;
                    w = 1LL * w * wn[id] % P;
                }
            }
        }
        if(on == -1) {
            for(int i = 1; i < len / 2; ++i) swap(y[i], y[len-i]);
            int inv = qpow(len, P - 2, P);
            for(int i = 0; i < len; ++i)
                y[i] = 1LL * y[i] * inv % P;
        }
    }

    //自动多项式乘法，结果将会反映到A数组
    //需要事先调整好len至大于离2n最近的2的幂
    void mul(int A[], int B[], int len) {
        NTT(A, len, 1);
        NTT(B, len, 1);
        for(int i = 0; i < len; ++i) A[i] = 1LL * A[i] * B[i] % P;
        NTT(A, len, -1);
    }
}ntt[K];

int tmp[MAXN][K], t1[MAXN], t2[MAXN];
int r[K][K];

//特殊的防爆CRT
//x = x0 + x1*p0 + x2*p0*p1 (% p0*p1*p2) [0<=x0<p0 0<=x1<p1 0<=x2<p2]
//x = a0 (% p0)
//x = a1 (% p1)
//x = a2 (% p2)

//因为我们保证p0*p1*p2>MODER*MODER*n，在P0*p1*p2模空间内，我们计算的原始数值一定只有单个映射
//我们的目的是求出x0 x1 x2,借此用另外一种形式表达x(p0p1p2混合进制形式)
//这样就可以绕开爆LL的问题

//x (%p0) = a0 (%p0) = x0 [因为x0的范围限定在[0,p0),可以看成求出了(% p0*p1*p2)中的x0]
//x (%p1) = a1 (%p1) = x0 + x1*p0 (%p1) [因为p1|p0*p1*p2,在大空间中的x0对应到小空间的位置是确定的]
// --> x1 = (a1 - x0)/p0 (%p1) [因为x1的范围限定在[0,p1),可以看成求出了(% p0*p1*p2)中的x1]
//x (%p2) = a2 (%p2) = x0 + x1*p0 + x2*p0*p1 (%p2) [同上]
// --> x2 = (a2 - x0 - x1*p0)/p0*p1 (%p2) [同上]

int CRT(int a[]) {
    int x[K];
    for(int i = 0; i < K; ++i) {
        x[i] = a[i];
        for(int j = 0; j < i; ++j) {
            int t = (x[i] - x[j]) % m[i];
            if(t < 0) t += m[i];
            x[i] = 1LL * t * r[j][i] % m[i];
        }
    }
    int mul = 1, ret = x[0] % MOD;
    for(int i = 1; i < K; ++i) {
        mul = 1LL * mul * m[i-1] % MOD;
        ret += 1LL * x[i] * mul % MOD;
        if(ret >= MOD) ret -= MOD;
    }
    return ret;
}

//自动多项式乘法，模指定的数(1e9+7)
//len需要调整到离2n最近的2的幂，下标从0开
//结果存入A[]中
//系数模1e9+7就可以
void mul(int A[], int B[], int len) {
    for(int id = 0; id < K; ++id) {
        //转储系数变量
        for(int i = 0; i < len; ++i) {
            t1[i] = A[i];
            t2[i] = B[i];
        }
        //使用id号NTT单元做多项式乘法
        ntt[id].mul(t1, t2, len);
        //转储乘法结果
        for(int i = 0; i < len; ++i)
            tmp[i][id] = t1[i];
    }
    //将乘法结果回射到指定(1e9+7)空间
    for(int i = 0; i < len; ++i) {
        A[i] = CRT(tmp[i]);
    }
}

//预处理逆元r[i][j]:m[i]在m[j]空间内逆元
//初始化需要的NTT单元
void init() {
    for(int i = 0; i < K; ++i) {
        for(int j = 0; j < i; ++j) {
            r[j][i] = qpow(m[j], m[i] - 2, m[i]);
        }
    }
    for(int i = 0; i < K; ++i) {
        ntt[i].init(m[i]);
    }
}

#endif

int N,M;
int hf[MAXN/2][MAXN/2];
void prephf2(){
    for(int w = 2;w < MAXN/2; w++){
        hf[1][w] = 1;
    }
    for(int h = 2;h < MAXN/2;h++){
        int pfx = 0;
        for(int w = 1;w < MAXN/2; w++){
            pfx = summod(pfx, hf[h-1][w],MOD);
            hf[h][w] = summod(hf[h][w-1], pfx,MOD);
        }
    }
}
int al[MAXN/2][MAXN/2];

int f[MAXN/2],g[MAXN/2],pfx[MAXN/2];
int ff[MAXN],gg[MAXN];
void prepal2(){
    for(int h = 1;h <= 2000; h++){
        al[h][2] = 1;
    }

    for (int w = 3; w <= 2000; w++) {
        f[0] = 0;
        g[0] = 1;
        for(int h = 1;h <= 2000; h++){
            f[h] = hf[h][w];
            pfx[h] = summod(pfx[h], hf[h][w-1], MOD);
            g[h] = summod(summod(pfx[h], g[h], MOD), hf[h][w-1], MOD);
        }
        memset(ff, 0, sizeof(ff));
        memset(gg, 0, sizeof(gg));
        for(int j = 0;j <= 2000; j++){
            ff[j] = f[j];
            gg[j] = g[j];
        }
        mul(ff, gg, 4096);
        for(int h = 0;h <= 2000; h++){
            al[h][w] = ff[h];
        }
    }
}

int main(int argc, const char * argv[]){
#ifdef LOCAL_DEBUG
    freopen("testdata.in", "r", stdin);
    clock_t clk = clock();
#endif

    init();
    prephf2();
    prepal2();
    while (cin >> N >> M) {
        LL res = 0;
        for(int h = N;h >= 1; h--){
            LL mpl = N-h+1;
            LL tmp = 0;
            for(int w = M;w >= 2;w--){
                LL mlp = M-w+1;
                tmp = summod(tmp, mulmod(mlp, al[h][w], MOD), MOD);
            }
            res = summod(res, mulmod(mpl, tmp, MOD), MOD);
        }
        cout << res << endl;
    }


#ifdef LOCAL_DEBUG
    puts("-----END OF OUTPUT-----");
    printf("Time Elapsed: %luMS\n",(clock() - clk)/CLK_TCK/10);
#endif

    return 0;
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

233

234

235

236

237

238

239

240

241

242

243

244

245

246

247

248

249

250

251

252

253

254

255

256

257

258

259

260

261

262

263

264

265

266

267

268

269

//NTT Version

//Warning:Severely Exceeds TL(14s,TL2s),although O(n^2logn)

#define REP(i,t) for(int i = 0;i < t; i++)

#define REP_1(i,t) for(int i = 1;i <= t; i++)

#define CASE_LOOP int ___;scanf(" %d",&___);for(int __ = 1; __ <= ___; __++)

#define FOR_EDGE(i,u) for (int i = head[u]; i; i = nxt[i])

#define ADHOC_CIN(typ,name) typ name;cin >> name;

#define ADHOC_SCANINT(name) int name;scanf(" %d",&name);

using namespace std;

typedef long long LL;

typedef long double LD;

#define USUAL_MODANY

#ifdef USUAL_MODANY

inline LL getmod(LL a,LL m){if(a<0||a>=m)a%=m;if(a<0)a+=m;return a;}

inline LL summod(LL a,LL b,LL m){return getmod(getmod(a,m)+getmod(b,m),m);}

inline LL mulmod(LL a,LL b,LL m){return getmod(getmod(a,m)*getmod(b,m),m);}

inline LL powmod(LL a,LL p,LL m){LL ret=1;while(p){if(p&1)ret=mulmod(ret,a,m);a=mulmod(a,a,m);p>>=1;}return ret;}

inline LL invmod(LL a,LL m){return powmod(a,m-2,m);}

#endif

#define NTT_MOD_ANY

#ifdef NTT_MOD_ANY

// 多项式乘法系数对MOD=1000000007取模，常数巨大，慎用

// 只要选的K个素数乘积大于MOD*MOD*N,理论上MOD可以任取。

#define MOD 1000000007

#define K 3

//用于CRT的三个模空间

const int m[K] = {1004535809, 998244353, 104857601};

//479*2^21+1,7*17*2^23+1,25*2^22+1

//m[0] > m[1] > m[2]

#define G 3

//上述三个素数的原根

const int MAXN = 4444;

inline int qpow(int x, int k, int P) {

int ret = 1;

while(k) {

if(k & 1) ret = 1LL * ret * x % P;

k >>= 1;

x = 1LL * x * x % P;

}

return ret;

}

struct _NTT {

//wn:旋转分量 P:模空间(P-1是2的幂)

int wn[25], P;

//init(_P)用给出的模空间_P构建旋转分量

void init(int _P) {

P = _P;

for(int i = 1; i <= 21; ++i) {

int t = 1 << i;

wn[i] = qpow(G, (P - 1) / t, P);

}

//RADAR编码

//FFT与IFFT之前的反转变换

//位置i和(i的二进制反转)位置互换

//len需要是2的幂

void change(int *y, int len) {

for(int i = 1, j = len / 2; i < len - 1; ++i) {

if(i < j) swap(y[i], y[j]);

int k = len / 2;

while(j >= k) {

j -= k;

k /= 2;

}

j += k;

}

//NTT主过程，y是等待变换的数组，下标从0开始，长度为len

//len是2的幂

//on=1的话NTT on=-1的话INTT

void NTT(int *y, int len, int on) {

change(y, len);

int id = 0;

for(int h = 2; h <= len; h <<= 1) {

++id;

for(int j = 0; j < len; j += h) {

int w = 1;

for(int k = j; k < j + h / 2; ++k) {

int u = y[k];

int t = 1LL * y[k+h/2] * w % P;

y[k] = u + t;

if(y[k] >= P) y[k] -= P;

y[k+h/2] = u - t + P;

if(y[k+h/2] >= P) y[k+h/2] -= P;

w = 1LL * w * wn[id] % P;

}

if(on == -1) {

for(int i = 1; i < len / 2; ++i) swap(y[i], y[len-i]);

int inv = qpow(len, P - 2, P);

for(int i = 0; i < len; ++i)

y[i] = 1LL * y[i] * inv % P;

}

//自动多项式乘法，结果将会反映到A数组

//需要事先调整好len至大于离2n最近的2的幂

void mul(int A[], int B[], int len) {

NTT(A, len, 1);

NTT(B, len, 1);

for(int i = 0; i < len; ++i) A[i] = 1LL * A[i] * B[i] % P;

NTT(A, len, -1);

}

}ntt[K];

int tmp[MAXN][K], t1[MAXN], t2[MAXN];

int r[K][K];

//特殊的防爆CRT

//x = x0 + x1*p0 + x2*p0*p1 (% p0*p1*p2) [0<=x0<p0 0<=x1<p1 0<=x2<p2]

//x = a0 (% p0)

//x = a1 (% p1)

//x = a2 (% p2)

//因为我们保证p0*p1*p2>MODER*MODER*n，在P0*p1*p2模空间内，我们计算的原始数值一定只有单个映射

//我们的目的是求出x0 x1 x2,借此用另外一种形式表达x(p0p1p2混合进制形式)

//这样就可以绕开爆LL的问题

//x (%p0) = a0 (%p0) = x0 [因为x0的范围限定在[0,p0),可以看成求出了(% p0*p1*p2)中的x0]

//x (%p1) = a1 (%p1) = x0 + x1*p0 (%p1) [因为p1|p0*p1*p2,在大空间中的x0对应到小空间的位置是确定的]

// --> x1 = (a1 - x0)/p0 (%p1) [因为x1的范围限定在[0,p1),可以看成求出了(% p0*p1*p2)中的x1]

//x (%p2) = a2 (%p2) = x0 + x1*p0 + x2*p0*p1 (%p2) [同上]

// --> x2 = (a2 - x0 - x1*p0)/p0*p1 (%p2) [同上]

int CRT(int a[]) {

int x[K];

for(int i = 0; i < K; ++i) {

x[i] = a[i];

for(int j = 0; j < i; ++j) {

int t = (x[i] - x[j]) % m[i];

if(t < 0) t += m[i];

x[i] = 1LL * t * r[j][i] % m[i];

}

int mul = 1, ret = x[0] % MOD;

for(int i = 1; i < K; ++i) {

mul = 1LL * mul * m[i-1] % MOD;

ret += 1LL * x[i] * mul % MOD;

if(ret >= MOD) ret -= MOD;

}

return ret;

}

//自动多项式乘法，模指定的数(1e9+7)

//len需要调整到离2n最近的2的幂，下标从0开

//结果存入A[]中

//系数模1e9+7就可以

void mul(int A[], int B[], int len) {

for(int id = 0; id < K; ++id) {

//转储系数变量

for(int i = 0; i < len; ++i) {

t1[i] = A[i];

t2[i] = B[i];

}

//使用id号NTT单元做多项式乘法

ntt[id].mul(t1, t2, len);

//转储乘法结果

for(int i = 0; i < len; ++i)

tmp[i][id] = t1[i];

}

//将乘法结果回射到指定(1e9+7)空间

for(int i = 0; i < len; ++i) {

A[i] = CRT(tmp[i]);

}

//预处理逆元r[i][j]:m[i]在m[j]空间内逆元

//初始化需要的NTT单元

void init() {

for(int i = 0; i < K; ++i) {

for(int j = 0; j < i; ++j) {

r[j][i] = qpow(m[j], m[i] - 2, m[i]);

}

for(int i = 0; i < K; ++i) {

ntt[i].init(m[i]);

}

#endif

int N,M;

int hf[MAXN/2][MAXN/2];

void prephf2(){

for(int w = 2;w < MAXN/2; w++){

hf[1][w] = 1;

}

for(int h = 2;h < MAXN/2;h++){

int pfx = 0;

for(int w = 1;w < MAXN/2; w++){

pfx = summod(pfx, hf[h-1][w],MOD);

hf[h][w] = summod(hf[h][w-1], pfx,MOD);

}

int al[MAXN/2][MAXN/2];

int f[MAXN/2],g[MAXN/2],pfx[MAXN/2];

int ff[MAXN],gg[MAXN];

void prepal2(){

for(int h = 1;h <= 2000; h++){

al[h][2] = 1;

}

for (int w = 3; w <= 2000; w++) {

f[0] = 0;

g[0] = 1;

for(int h = 1;h <= 2000; h++){

f[h] = hf[h][w];

pfx[h] = summod(pfx[h], hf[h][w-1], MOD);

g[h] = summod(summod(pfx[h], g[h], MOD), hf[h][w-1], MOD);

}

memset(ff, 0, sizeof(ff));

memset(gg, 0, sizeof(gg));

for(int j = 0;j <= 2000; j++){

ff[j] = f[j];

gg[j] = g[j];

}

mul(ff, gg, 4096);

for(int h = 0;h <= 2000; h++){

al[h][w] = ff[h];

}

int main(int argc, const char * argv[]){

#ifdef LOCAL_DEBUG

freopen("testdata.in", "r", stdin);

clock_t clk = clock();

#endif

init();

prephf2();

prepal2();

while (cin >> N >> M) {

LL res = 0;

for(int h = N;h >= 1; h--){

LL mpl = N-h+1;

LL tmp = 0;

for(int w = M;w >= 2;w--){

LL mlp = M-w+1;

tmp = summod(tmp, mulmod(mlp, al[h][w], MOD), MOD);

}

res = summod(res, mulmod(mpl, tmp, MOD), MOD);

}

cout << res << endl;

}

#ifdef LOCAL_DEBUG

puts("-----END OF OUTPUT-----");

printf("Time Elapsed: %luMS\n",(clock() - clk)/CLK_TCK/10);

#endif

return 0;

}

正解

//Accepted Version
//Enumerate w
//Enumerate upper part (xxxx5)
//preCalculate lower part (4xxx) product times
//This can make in O(n^2) time
//No NTT required
#define REP(i,t) for(int i = 0;i < t; i++)
#define REP_1(i,t) for(int i = 1;i <= t; i++)
#define CASE_LOOP int ___;scanf(" %d",&___);for(int __ = 1; __ <= ___; __++)
#define FOR_EDGE(i,u) for (int i = head[u]; i; i = nxt[i])
#define ADHOC_CIN(typ,name) typ name;cin >> name;
#define ADHOC_SCANINT(name) int name;scanf(" %d",&name);

using namespace std;

typedef long long LL;
typedef long double LD;

#define USUAL_MOD1E9
#ifdef USUAL_MOD1E9
const LL MODER = 1000000007;
LL getmod(LL a){if(a<0||a>=MODER)a%=MODER;if(a<0)a+=MODER;return a;}
LL summod(LL a,LL b){return getmod(getmod(a)+getmod(b));}
LL mulmod(LL a,LL b){return getmod(getmod(a)*getmod(b));}
LL powmod(LL a,LL p){LL ret=1;while(p){if(p&1)ret=mulmod(ret,a);a=mulmod(a,a);p>>=1;}return ret;}
LL invmod(LL a){return powmod(a,MODER-2);}
#endif

const int MAXN = 2005;
int N,M;
int hf[MAXN][MAXN];
void prephf(){
    for(int w = 2;w < MAXN; w++){
        hf[1][w] = 1;
    }
    for(int h = 2;h < MAXN;h++){
        int pfx = 0;
        for(int w = 1;w < MAXN; w++){
            pfx = summod(pfx, hf[h-1][w]);
            hf[h][w] = summod(hf[h][w-1], pfx);
        }
    }
}
int lower[MAXN][MAXN];
void preplower(){
    REP_1(h, MAXN-1){
        int pfx = 0;
        for(int w = 2;w < MAXN; w++){
            pfx = summod(pfx, hf[h][w]);
            lower[h][w] = summod(lower[h][w-1], summod(pfx, hf[h][w]));
        }
    }
}
int sml[MAXN][MAXN];
void prepsml(){
    REP_1(w, MAXN-1){
        int pfx = 0;
        REP_1(h, MAXN-1){
            pfx = summod(pfx,lower[h][w]);
            sml[h][w] = summod(sml[h-1][w], pfx);
        }
    }
}

void prep(){
    prephf();
    preplower();
    prepsml();
}

void solve(){
    int res = 0;
    REP_1(w, M){
        int tim = M+1-w;
        int tmp = 0;
        REP_1(upper, N){
            tmp = summod(tmp, mulmod(hf[upper][w], (N+1-upper)));
            tmp = summod(tmp, mulmod(hf[upper][w], sml[N-upper][w-1]));
        }
        res = summod(res, mulmod(tmp, tim));
    }
    cout << res << endl;
}

int main(int argc, const char * argv[]){
#ifdef LOCAL_DEBUG
    freopen("testdata.in", "r", stdin);
    clock_t clk = clock();
#endif

    prep();
    while (cin >> N >> M) {
        solve();
    }

#ifdef LOCAL_DEBUG
    puts("-----END OF OUTPUT-----");
    printf("Time Elapsed: %luMS\n",(clock() - clk)/CLK_TCK/10);
#endif

    return 0;
}

100

101

102

//Accepted Version

//Enumerate w

//Enumerate upper part (xxxx5)

//preCalculate lower part (4xxx) product times

//This can make in O(n^2) time

//No NTT required

#define REP(i,t) for(int i = 0;i < t; i++)

#define REP_1(i,t) for(int i = 1;i <= t; i++)

#define CASE_LOOP int ___;scanf(" %d",&___);for(int __ = 1; __ <= ___; __++)

#define FOR_EDGE(i,u) for (int i = head[u]; i; i = nxt[i])

#define ADHOC_CIN(typ,name) typ name;cin >> name;

#define ADHOC_SCANINT(name) int name;scanf(" %d",&name);

using namespace std;

typedef long long LL;

typedef long double LD;

#define USUAL_MOD1E9

#ifdef USUAL_MOD1E9

const LL MODER = 1000000007;

LL getmod(LL a){if(a<0||a>=MODER)a%=MODER;if(a<0)a+=MODER;return a;}

LL summod(LL a,LL b){return getmod(getmod(a)+getmod(b));}

LL mulmod(LL a,LL b){return getmod(getmod(a)*getmod(b));}

LL powmod(LL a,LL p){LL ret=1;while(p){if(p&1)ret=mulmod(ret,a);a=mulmod(a,a);p>>=1;}return ret;}

LL invmod(LL a){return powmod(a,MODER-2);}

#endif

const int MAXN = 2005;

int N,M;

int hf[MAXN][MAXN];

void prephf(){

for(int w = 2;w < MAXN; w++){

hf[1][w] = 1;

}

for(int h = 2;h < MAXN;h++){

int pfx = 0;

for(int w = 1;w < MAXN; w++){

pfx = summod(pfx, hf[h-1][w]);

hf[h][w] = summod(hf[h][w-1], pfx);

}

int lower[MAXN][MAXN];

void preplower(){

REP_1(h, MAXN-1){

int pfx = 0;

for(int w = 2;w < MAXN; w++){

pfx = summod(pfx, hf[h][w]);

lower[h][w] = summod(lower[h][w-1], summod(pfx, hf[h][w]));

}

int sml[MAXN][MAXN];

void prepsml(){

REP_1(w, MAXN-1){

int pfx = 0;

REP_1(h, MAXN-1){

pfx = summod(pfx,lower[h][w]);

sml[h][w] = summod(sml[h-1][w], pfx);

}

void prep(){

prephf();

preplower();

prepsml();

}

void solve(){

int res = 0;

REP_1(w, M){

int tim = M+1-w;

int tmp = 0;

REP_1(upper, N){

tmp = summod(tmp, mulmod(hf[upper][w], (N+1-upper)));

tmp = summod(tmp, mulmod(hf[upper][w], sml[N-upper][w-1]));

}

res = summod(res, mulmod(tmp, tim));

}

cout << res << endl;

}

int main(int argc, const char * argv[]){

#ifdef LOCAL_DEBUG

freopen("testdata.in", "r", stdin);

clock_t clk = clock();

#endif

prep();

while (cin >> N >> M) {

solve();

}

#ifdef LOCAL_DEBUG

puts("-----END OF OUTPUT-----");

printf("Time Elapsed: %luMS\n",(clock() - clk)/CLK_TCK/10);

#endif

return 0;

}

参考

kmjpさん（日本語注意）：
http://kmjp.hatenablog.jp/entry/2014/09/22/0900

Zeyu_king：
http://blog.csdn.net/zeyu_king/article/details/44040749

后缀数组

September 17, 20162016-09-17hahaschoolLeave a comment

构造后缀数组

倍增前缀法

#define SUFFIX_ARRAY_PFXDBL
#ifdef SUFFIX_ARRAY_PFXDBL
namespace SA{
    /*
     Suffix Array, Prefix Doubling Method

     <SUBSCRIPT_START_FROM,SIZE>
     MAXN   : Maximum length for string
     s      : String for building suffix array <0,MAXN>
     t,t2,c : [Auxiliary] buffers <0,MAXN>
     n      : Length of string

     sa     : Suffix Array, Lexicographically ith suffix starts from.  <0,MAXN>
     rank   : Suffix Rank, rank of the suffix starts from i <0,MAXN>
     height : LCP of suffix starts from sa[i] and sa[i-1] <1,MAXN>

     build_sa(int m) : m is the size of character set("character" being 0~m-1), should set s and n previously.
     getHeight() : Calculate height and rank array accordingly.

     #define REP(i,t) for(int i = 0;i < t; i++)
     #define REP_R(i,t) for(int i = t-1;i >= 0; i--)
     #define REP_1(i,t) for(int i = 1;i <= t; i++)
     #define REP_1R(i,t) for(int i = t;i >= 1; i--)

     Time   : O(nlogn)
     Space  : 7n
     */
    const int MAXN = 10005;
    char s[MAXN];
    int sa[MAXN],t[MAXN],t2[MAXN],c[MAXN],rank[MAXN],height[MAXN],n;
    void build_sa(int m){
        int *x = t,*y = t2;
        //第一次基数排序
        REP(i, m) c[i] = 0; //重置排序数组
        REP(i, n) c[x[i]=s[i]]++; //拷贝字符串内容到x缓冲区，并在基数排序数组中统计字符数量
        REP_1(i, m-1) c[i] += c[i-1]; //基数排序数组求前缀和以算出排名
        REP_R(i, n-1) sa[--c[x[i]]] = i; //从后往前顺次查询后缀的排名写入SA(字符相同的时候，长度小的靠前，长度大的靠后)
        //此时的x数组可以看成是保存了各个位置开始的后缀对应的第一基准
        for(int k = 1;k <= n; k <<= 1){
            //第k次基数排序,单组长度2^k
            int p = 0;
            //利用SA排序第二基准，y存储的是第二基准排序之后的后缀开始位置
            for(int i = n-k;i < n; i++) y[p++] = i; //长度没达到k，这种只能看第一基准，第二基准视为0
            REP(i, n) if(sa[i] >= k) y[p++] = sa[i]-k; //从前往后扫SA，即从字典序小的后缀开始扫，如果这个后缀的开始位置>=k的话，这个后缀在sa中的结果实际上是i-k的第二基准
            //排序第一基准
            REP(i, m) c[i] = 0; //重置排序数组
            REP(i, n) c[x[y[i]]]++; //按第二基准顺序读取第一基准进行统计
            REP(i, m) c[i] += c[i-1];//基数排序数组求前缀和以算出排名
            REP_R(i, n-1) sa[--c[x[y[i]]]] = y[i];//按第二基准从后往前顺次查询后缀的排名写入SA
            //准备下一次排序的第一基准序列x
            //第二基准排序结果y没有用了，上一次的第一基准序列x还有用，直接互换
            swap(x, y);
            //现在y是上一次的第一基准序列
            p = 1;
            x[sa[0]] = 0;//第一基准从0开始
            //现在的sa是排好序的，从小到大查询，如果两项无法分出先后，就令成统一基准，否则基准自增
            REP_1(i, n-1) x[sa[i]] = ((y[sa[i-1]] == y[sa[i]]) && (y[sa[i-1]+k]==y[sa[i]+k]))? p-1 : p++;
            if(p >= n) break; //如果基准数已达n，说明排序完成，所有后缀已经分出先后
            m = p; //下一轮排序的基准数是p
        }
    }
    void getHeight(){
        int i,j,k = 0;
        REP(i, n) rank[sa[i]] = i;
        for(i = 0;i < n; height[rank[i++]] = k)
            for(k?k--:0,j = sa[rank[i]-1];s[i+k]==s[j+k];k++);
        return;
    }
}
#endif

#define SUFFIX_ARRAY_PFXDBL

#ifdef SUFFIX_ARRAY_PFXDBL

namespace SA{

Suffix Array, Prefix Doubling Method

<SUBSCRIPT_START_FROM,SIZE>

MAXN : Maximum length for string

s : String for building suffix array <0,MAXN>

t,t2,c : [Auxiliary] buffers <0,MAXN>

n : Length of string

sa : Suffix Array, Lexicographically ith suffix starts from. <0,MAXN>

rank : Suffix Rank, rank of the suffix starts from i <0,MAXN>

height : LCP of suffix starts from sa[i] and sa[i-1] <1,MAXN>

build_sa(int m) : m is the size of character set("character" being 0~m-1), should set s and n previously.

getHeight() : Calculate height and rank array accordingly.

#define REP(i,t) for(int i = 0;i < t; i++)

#define REP_R(i,t) for(int i = t-1;i >= 0; i--)

#define REP_1(i,t) for(int i = 1;i <= t; i++)

#define REP_1R(i,t) for(int i = t;i >= 1; i--)

Time : O(nlogn)

Space : 7n

const int MAXN = 10005;

char s[MAXN];

int sa[MAXN],t[MAXN],t2[MAXN],c[MAXN],rank[MAXN],height[MAXN],n;

void build_sa(int m){

int *x = t,*y = t2;

//第一次基数排序

REP(i, m) c[i] = 0; //重置排序数组

REP(i, n) c[x[i]=s[i]]++; //拷贝字符串内容到x缓冲区，并在基数排序数组中统计字符数量

REP_1(i, m-1) c[i] += c[i-1]; //基数排序数组求前缀和以算出排名

REP_R(i, n-1) sa[--c[x[i]]] = i; //从后往前顺次查询后缀的排名写入SA(字符相同的时候，长度小的靠前，长度大的靠后)

//此时的x数组可以看成是保存了各个位置开始的后缀对应的第一基准

for(int k = 1;k <= n; k <<= 1){

//第k次基数排序,单组长度2^k

int p = 0;

//利用SA排序第二基准，y存储的是第二基准排序之后的后缀开始位置

for(int i = n-k;i < n; i++) y[p++] = i; //长度没达到k，这种只能看第一基准，第二基准视为0

REP(i, n) if(sa[i] >= k) y[p++] = sa[i]-k; //从前往后扫SA，即从字典序小的后缀开始扫，如果这个后缀的开始位置>=k的话，这个后缀在sa中的结果实际上是i-k的第二基准

//排序第一基准

REP(i, m) c[i] = 0; //重置排序数组

REP(i, n) c[x[y[i]]]++; //按第二基准顺序读取第一基准进行统计

REP(i, m) c[i] += c[i-1];//基数排序数组求前缀和以算出排名

REP_R(i, n-1) sa[--c[x[y[i]]]] = y[i];//按第二基准从后往前顺次查询后缀的排名写入SA

//准备下一次排序的第一基准序列x

//第二基准排序结果y没有用了，上一次的第一基准序列x还有用，直接互换

swap(x, y);

//现在y是上一次的第一基准序列

p = 1;

x[sa[0]] = 0;//第一基准从0开始

//现在的sa是排好序的，从小到大查询，如果两项无法分出先后，就令成统一基准，否则基准自增

REP_1(i, n-1) x[sa[i]] = ((y[sa[i-1]] == y[sa[i]]) && (y[sa[i-1]+k]==y[sa[i]+k]))? p-1 : p++;

if(p >= n) break; //如果基准数已达n，说明排序完成，所有后缀已经分出先后

m = p; //下一轮排序的基准数是p

}

void getHeight(){

int i,j,k = 0;

REP(i, n) rank[sa[i]] = i;

for(i = 0;i < n; height[rank[i++]] = k)

for(k?k--:0,j = sa[rank[i]-1];s[i+k]==s[j+k];k++);

return;

}

#endif

DC3

#define SUFFIX_ARRAY_DC3
#ifdef SUFFIX_ARRAY_DC3
namespace SA{
    /*
     Suffix Array, DC3 Method
     <SUBSCRIPT_START_FROM,SIZE>
     MAXN   : Maximum length of string
     wa,wb  : [Auxiliary] buffer <0,MAXN>
     wv,ws  : [Auxiliary] buffer <0,MAXN>

     rank   : Suffix Rank, rank of the suffix starts from i <0,MAXN>
     height : LCP of suffix starts from sa[i] and sa[i-1] <1,MAXN>

     sort() : [Auxiliary] Radix sort
     c0()   : [Auxiliary] Checker for same rank character tuple
     c12()  : [Auxiliary] Comparer in the merging process
     F()    : [Auxiliary] Find suffix(x)'s new position
     G()    : [Auxiliary] Find suffix(x)'s original position

     dc3(r,sa,n,m) : Build Suffix Array using DC3 method :
     r  : String used to build Suffix Array <0,MAXN*3>
     sa : Suffix Array, Lexicographically ith suffix starts from.  <0,MAXN*3>
     n  : String length
     m  : Character set size
     ATTENTION : characters in string r should be 1~m and r should be ended with 0.
     getHeight(r,sa,n) : Get rank and height arrary for given string r and corrsponding Suffix Array sa.

     #define REP(i,t) for(int i = 0;i < t; i++)
     #define REP_R(i,t) for(int i = t-1;i >= 0; i--)
     #define REP_1(i,t) for(int i = 1;i <= t; i++)
     #define REP_1R(i,t) for(int i = t;i >= 1; i--)

     Time   : O(n)
     Space  : 12n
     */

    const int MAXN = 10005;
    int wa[MAXN],wb[MAXN],wv[MAXN],ws[MAXN];
    inline int c0(int *r,int a,int b){
        return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];
    }
    inline int c12(int k,int *r,int a,int b){
        if(k==2) return r[a] < r[b] || (r[a] == r[b] && c12(1,r,a+1,b+1));
        else     return r[a] < r[b] || (r[a] == r[b] && wv[a+1] < wv[b+1]);
    }
    void sort(int *r,int *a,int *b,int n,int m){
        /*
         基数排序,b是a中的位置按对应的r中字符大小排序之后的结果
         r : 字符串
         a : 要排序的项目在字符串上的位置
         b : 排序的结果要存储到的数组
         n : 要排序的项目总数
         m : 字符集大小
         */
        REP(i, n) wv[i] = r[a[i]];//从字符串中抽出要排序的项目到wv
        REP(i, m) ws[i] = 0;//重置基数排序数组
        REP(i, n) ws[wv[i]]++;//统计各种字符的数量
        REP_1(i, m-1) ws[i] += ws[i-1];//计算基数排序数组的前缀和以确定排名
        REP_R(i, n-1) b[--ws[wv[i]]] = a[i];//把排序结果写入b数组
    }

    inline int F(const int x,const int tb){
        return x/3 + ((x%3==1)?0:tb);
    }
    inline int G(const int x,const int tb){
        return (x<tb)?(x*3+1):((x-tb)*3+2);
    }
    void dc3(int *r,int *sa,int n,int m){
        /*
         rn  : 要递归处理的新字符串
         san : 新字符串对应的后缀数组
         ta  : 起始位置模3为0的后缀总数
         tb  : 起始位置模3为1的后缀总数
         tbc : 起始位置模3为1或2的后缀总数
         */
        int *rn = r+n, *san = sa+n, ta = 0, tb = (n+1)/3, tbc = 0, p;

        //PART1: 计算好起始位置模3不等于0的后缀的对应的SA
        //用基数排序把3个字符合并成一个字符
        r[n] = r[n+1] = 0;
        REP(i, n) if(i%3) wa[tbc++] = i;//记录起始位置模3不为0的后缀到wa中
        sort(r+2, wa, wb, tbc, m);//以第三个字符为基准排序
        sort(r+1, wb, wa, tbc, m);//在三准基础上以第二个字符为基准排序
        sort(r, wa, wb, tbc, m);//在二三准基础上以第一个字符为基准排序
        //这样就完成了三个字符的合并
        //根据排序结果求新的字符串
        //F(x) : 计算原字符串起始位置是x的后缀在新字符串中的起始位置
        //c0() : 判定两个字符组是否完全一致
        int i,j;
        for(p = 1,rn[F(wb[0],tb)] = 0,i = 1;i < tbc; i++)
            rn[F(wb[i],tb)] = c0(r, wb[i-1], wb[i])? (p-1):(p++);

        if(p < tbc)
            //递归处理新字符串(有些字符组无法区分)
            dc3(rn, san, tbc, p);
        else
            //可以直接求出san的情形(所有的字符组可以区分)
            REP(i, tbc) san[rn[i]] = i;

        //PART2: 计算好起始位置模3等于0的后缀对应的SA
        //第二基准的排序结果可以藉由san直接得到
        REP(i, tbc) if(san[i] < tb) wb[++ta] = san[i]*3;
        if(n%3 == 1) wb[ta++] = n-1;//san中没有n-1，所以要特殊处理
        sort(r, wb, wa, ta, m);//第一基准为新加的字符，在算好的第二基准基础上排序
        //把san中的结果做一个反射，因为我们接下来要查询在新字符串中的以x结尾的后缀的排名是多少
        //G(x): 计算新字符串中起始位置为x的后缀在原字符串中的位置
        REP(i, tbc) wv[wb[i] = G(san[i],tb)] = i;

        //PART3: 合并前面两部分的结果
        //c12(): 合并时使用的比较
        for(i = j = p = 0;i < ta && j < tbc; p++)
            sa[p] = c12(wb[j]%3, r, wa[i], wb[j])?wa[i++] : wb[j++];
        for(;i < ta; p++) sa[p] = wa[i++];
        for(;j < tbc; p++) sa[p] = wb[j++];
    }

    int rank[MAXN],height[MAXN];
    void getHeight(int *r,int *sa,int n){
        int i,j,k = 0;
        REP(i, n) rank[sa[i]] = i;
        for(i = 0;i < n; height[rank[i++]] = k)
            for(k?k--:0,j = sa[rank[i]-1];r[i+k]==r[j+k];k++);
        return;
    }


}

#endif

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

#define SUFFIX_ARRAY_DC3

#ifdef SUFFIX_ARRAY_DC3

namespace SA{

Suffix Array, DC3 Method

<SUBSCRIPT_START_FROM,SIZE>

MAXN : Maximum length of string

wa,wb : [Auxiliary] buffer <0,MAXN>

wv,ws : [Auxiliary] buffer <0,MAXN>

rank : Suffix Rank, rank of the suffix starts from i <0,MAXN>

height : LCP of suffix starts from sa[i] and sa[i-1] <1,MAXN>

sort() : [Auxiliary] Radix sort

c0() : [Auxiliary] Checker for same rank character tuple

c12() : [Auxiliary] Comparer in the merging process

F() : [Auxiliary] Find suffix(x)'s new position

G() : [Auxiliary] Find suffix(x)'s original position

dc3(r,sa,n,m) : Build Suffix Array using DC3 method :

r : String used to build Suffix Array <0,MAXN*3>

sa : Suffix Array, Lexicographically ith suffix starts from. <0,MAXN*3>

n : String length

m : Character set size

ATTENTION : characters in string r should be 1~m and r should be ended with 0.

getHeight(r,sa,n) : Get rank and height arrary for given string r and corrsponding Suffix Array sa.

#define REP(i,t) for(int i = 0;i < t; i++)

#define REP_R(i,t) for(int i = t-1;i >= 0; i--)

#define REP_1(i,t) for(int i = 1;i <= t; i++)

#define REP_1R(i,t) for(int i = t;i >= 1; i--)

Time : O(n)

Space : 12n

const int MAXN = 10005;

int wa[MAXN],wb[MAXN],wv[MAXN],ws[MAXN];

inline int c0(int *r,int a,int b){

return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];

}

inline int c12(int k,int *r,int a,int b){

if(k==2) return r[a] < r[b] || (r[a] == r[b] && c12(1,r,a+1,b+1));

else return r[a] < r[b] || (r[a] == r[b] && wv[a+1] < wv[b+1]);

}

void sort(int *r,int *a,int *b,int n,int m){

基数排序,b是a中的位置按对应的r中字符大小排序之后的结果

r : 字符串

a : 要排序的项目在字符串上的位置

b : 排序的结果要存储到的数组

n : 要排序的项目总数

m : 字符集大小

REP(i, n) wv[i] = r[a[i]];//从字符串中抽出要排序的项目到wv

REP(i, m) ws[i] = 0;//重置基数排序数组

REP(i, n) ws[wv[i]]++;//统计各种字符的数量

REP_1(i, m-1) ws[i] += ws[i-1];//计算基数排序数组的前缀和以确定排名

REP_R(i, n-1) b[--ws[wv[i]]] = a[i];//把排序结果写入b数组

}

inline int F(const int x,const int tb){

return x/3 + ((x%3==1)?0:tb);

}

inline int G(const int x,const int tb){

return (x<tb)?(x*3+1):((x-tb)*3+2);

}

void dc3(int *r,int *sa,int n,int m){

rn : 要递归处理的新字符串

san : 新字符串对应的后缀数组

ta : 起始位置模3为0的后缀总数

tb : 起始位置模3为1的后缀总数

tbc : 起始位置模3为1或2的后缀总数

int *rn = r+n, *san = sa+n, ta = 0, tb = (n+1)/3, tbc = 0, p;

//PART1: 计算好起始位置模3不等于0的后缀的对应的SA

//用基数排序把3个字符合并成一个字符

r[n] = r[n+1] = 0;

REP(i, n) if(i%3) wa[tbc++] = i;//记录起始位置模3不为0的后缀到wa中

sort(r+2, wa, wb, tbc, m);//以第三个字符为基准排序

sort(r+1, wb, wa, tbc, m);//在三准基础上以第二个字符为基准排序

sort(r, wa, wb, tbc, m);//在二三准基础上以第一个字符为基准排序

//这样就完成了三个字符的合并

//根据排序结果求新的字符串

//F(x) : 计算原字符串起始位置是x的后缀在新字符串中的起始位置

//c0() : 判定两个字符组是否完全一致

int i,j;

for(p = 1,rn[F(wb[0],tb)] = 0,i = 1;i < tbc; i++)

rn[F(wb[i],tb)] = c0(r, wb[i-1], wb[i])? (p-1):(p++);

if(p < tbc)

//递归处理新字符串(有些字符组无法区分)

dc3(rn, san, tbc, p);

else

//可以直接求出san的情形(所有的字符组可以区分)

REP(i, tbc) san[rn[i]] = i;

//PART2: 计算好起始位置模3等于0的后缀对应的SA

//第二基准的排序结果可以藉由san直接得到

REP(i, tbc) if(san[i] < tb) wb[++ta] = san[i]*3;

if(n%3 == 1) wb[ta++] = n-1;//san中没有n-1，所以要特殊处理

sort(r, wb, wa, ta, m);//第一基准为新加的字符，在算好的第二基准基础上排序

//把san中的结果做一个反射，因为我们接下来要查询在新字符串中的以x结尾的后缀的排名是多少

//G(x): 计算新字符串中起始位置为x的后缀在原字符串中的位置

REP(i, tbc) wv[wb[i] = G(san[i],tb)] = i;

//PART3: 合并前面两部分的结果

//c12(): 合并时使用的比较

for(i = j = p = 0;i < ta && j < tbc; p++)

sa[p] = c12(wb[j]%3, r, wa[i], wb[j])?wa[i++] : wb[j++];

for(;i < ta; p++) sa[p] = wa[i++];

for(;j < tbc; p++) sa[p] = wb[j++];

}

int rank[MAXN],height[MAXN];

void getHeight(int *r,int *sa,int n){

int i,j,k = 0;

REP(i, n) rank[sa[i]] = i;

for(i = 0;i < n; height[rank[i++]] = k)

for(k?k--:0,j = sa[rank[i]-1];r[i+k]==r[j+k];k++);

return;

}

#endif

经典问题

最长公共前缀(LCP)

可重叠最长重复子串

不可重叠最长重复子串

可重叠k次重复最长子串

不相同子串数目

最长回文子串

最长循环节

重复次数最多的循环节

最长公共子串

长度不小于k的公共子串个数

在至少k个字符串中出现的最长子串

每个字符串至少出现两次且不重叠的最长子串

出现或反转后出现在每个字符串中的最长子串

单模式串匹配问题与KMP算法

September 17, 20162016-09-17hahaschoolLeave a comment

单模式串匹配问题

问题定义

给出一个字符串T，称为模式串，再给出一个字符串S，称为原串，问模式串在原串中是否出现，出现位置都有哪些？

举个例子，T = “ha” ，S = “hahaschool” ,T在S中出现了两次，分别是S[0~1]和S[2~3]（下标从0开始）。

朴素解法

很简单，只要枚举T在S中出现位置的起点和终点，然后再逐位把S中的字符和T中对应位置的字符比对，如果全部对应，就说明T在S的该段匹配。

优化解法

在暴力匹配中，如果发生了失配（S中的字符不等于T中对应位置的字符），那么我们将会放弃当前的匹配进度，直接从S的下一位开始匹配。如果我们可以保留一部分的匹配进度，就可以减少计算量。这种想法就是我们接下来要讲的KMP算法的源头。

KMP算法

求Next数组

const int MAXN = 1005;
int nxt[MAXN];
void getNext (char *s, int len) {
    int i = 0, j = -1;
    nxt[0] = -1;
    while( i < len ) {
        if( j < 0 || s[i] == s[j] ) {
            ++i, ++j;
            if( s[i] == s[j] ) nxt[i] = nxt[j];
            else nxt[i] = j;
        }
        else j = nxt[j];
    }
}

const int MAXN = 1005;

int nxt[MAXN];

void getNext (char *s, int len) {

int i = 0, j = -1;

nxt[0] = -1;

while( i < len ) {

if( j < 0 || s[i] == s[j] ) {

++i, ++j;

if( s[i] == s[j] ) nxt[i] = nxt[j];

else nxt[i] = j;

}

else j = nxt[j];

}

使用Next数组加速字符串匹配

void KMP(char *t , char *s) {
    int tlen = strlen(t), slen = strlen(s);
    getNext (s,slen);
    int i = 0, j = 0;
    while( i < tlen ) {
        if( j < 0 || t[i] == s[j] ) {
            ++i, ++j;
        }
        else j = nxt[j];
    }
    if( j <= 0 ) {
        puts("0");
    }else {
        for( int i = 0; i < j; ++i )
            putchar( s[i] );
        putchar( ' '  );
        printf("%d\n", j );
    }
}

void KMP(char *t , char *s) {

int tlen = strlen(t), slen = strlen(s);

getNext (s,slen);

int i = 0, j = 0;

while( i < tlen ) {

if( j < 0 || t[i] == s[j] ) {

++i, ++j;

}

else j = nxt[j];

}

if( j <= 0 ) {

puts("0");

}else {

for( int i = 0; i < j; ++i )

putchar( s[i] );

putchar( ' ' );

printf("%d\n", j );

}

Next数组的其他应用

最长循环节

结合动态规划

Extended KMP

最长回文子串和Manacher算法

September 17, 20162017-05-05hahaschoolLeave a comment

最长回文子串

问题定义

给出一个字符串，找出其中的最长回文子串。

“回文串”是指，这个字符串从前往后读，和从后往前读效果是一样的。

比如”testset”、”hahaschooloohcsahah”，这样的串都是回文串。

子串是指在字符串中抽出的一段连续的字符，比如”school”是”hahaschool”的一个子串，”hsol”并不是”hahaschool”的子串，因为在原串中的对应位置不连续，”poi”也不是”hahaschool”的子串，因为无法在原始串中无法找到’p’和’i’。

朴素解法

解法一

枚举最长的回文串的长度len，在原始串中枚举len长度的子串，然后判断该子串是否为回文串，如果是的话更新答案。

时间代价：枚举长度O(n) * 枚举子串O(n) * 判断回文O(n) –> O(n^3)

解法二

枚举最长回文子串的中心center，然后尝试扩张以center为中心的回文子串(检查两边的字符是否相等，是的话扩张，否则停止)到最大，然后更新答案。

时间代价：枚举中心O(2n)=O(n) * 扩张O(n) –> O(n^2)

优化解法

解法三

分奇偶二分最长回文子串长度len。

检查len是否可行的方法是：然后枚举len长度的回文串的中心位置，然后判断是否回文。

时间代价：二分答案O(2logn)=O(logn) * 检查可行性O(n) * 回文判断O(n) –> O(n^2 logn)

看起来比解法二还慢，我们可以再加一个优化：利用Rabin-Karp方法哈希原始串和原始串反向串，通过判断回文串的左半部分的哈希值是否等于反向的右半部分哈希值，就可以判断是否回文，这样就可以实现回文判断的O(1)。

时间代价：二分答案O(2logn)=O(logn) * 检查可行性O(n) * 回文判断O(1) –> O(n logn)

解法四

首先，回文子串的左半部分是原始串的一个后缀，右半部分是原始串的反向串的一个后缀。

使用后缀数组，首先把原始串和原始串的反向串中间用一个特殊字符(只要字符串中没有出现过就可以，比如’#’)链接，然后求出链接后的串的后缀数组和LCP数组(height)。

接下来，只要枚举回文串的中心center，然后在利用LCP数组查询center对应的原始串后缀和反串后缀的LCP即可。

时间代价：后缀数组O(nlogn)或O(n) + 枚举中心O(n) * 求LCP O(logn) –> O(nlogn)

解法五

就是我们接下来要讨论的Manacher算法，可以达到O(n)的时间复杂度下界。

Manacher算法

开始之前的一些定义

我们的数组下标都是从0开始
我们接下来将称呼原始串为T
我们知道，回文子串的中心位置可能是一个字符本身，也可能是两个字符之间的空隙，所以我们接下来将把T做一些改动，即在每个字母的前后插入一个特殊字符’|’来表示字符间的空隙，如”abababa”，将会变成”|a|b|a|b|a|b|a|”，我们令这个改动后的串为S。简单观察一下，我们就可以发现，S的长度len(S) = len(T) * 2。
我们定义数组rad[]，rad[center]表示以center为中心的回文串的回文半径，其中center对应S的下标。举个例子，”|a|b|a|b|a|”，rad[0] = 0(分割线暂时忽略)，rad[1] = 1(“a”构成回文)，rad[5] = 5(“a|b|a|b|a”构成回文)。

为了更好地理解上述定义，再附两个例子：

lps13

lps12

我们接下来的目标就是在线性时间内算出rad[]的值。

先来找找规律

先来看一个例子：”abaaba”

Manacher3

观察图中标示出来的回文子串，发现什么了？

rad[2] = rad[4] = 0
rad[1] = rad[5] = 1

如果我们知道了rad[1]、rad[2]、rad[3]的值，那么我们就不用再去算rad[4]和rad[5]了，因为它们等于子串中心3左边的对应的点的rad值。

然后再观察以6为中心的回文子串，你会发现：

rad[5] = rad[7]
rad[4] = rad[8]
…

也就是说如果我们已经知道了rad[1~6]的值，rad[7~11]的值就不用额外算了，他们都可以对应到以6为中心的回文串的左半部分。

那我们再来看一个例子:”abababa”

Manacher4

按照上个例子那样，注意图中的标示，我们发现rad[1~6]可以和rad[8~13]对应上。

看起来在回文串的中心两边的rad值是对称的。然而这一点并不是一直成立
。我们注意当前这个例子的位置3和位置11，我们发现这两个位置对应的回文串内部并没有刚才那样的对称关系。

这给了我们一个提示，也许有没有这种对称关系取决于某种条件，当这种条件满足的时候，就可以通过对称关系来减少计算量，从而达到线性时间复杂度。如果条件不满足的话，就需要暴力判断。

那么我们接下来的目标就是探索这个规律。

在深入问题之前的补充定义

在深入问题之前，需要补充一些新的定义：
manacher5

中心位置centerPos：在中心位置的rad已经算好，我们令rad[centerPos]为d
右边界centerR：在中心位置右侧距离中心位置d单位远的位置，即中心位置所示的回文串的右边界，centerR = centerPos + d
左边界centerL：在中心位置左侧距离中心位置d单位远的位置，即中心位置所示的回文串的右边界，centerR = centerPos – d
当前处理位置curR：在中心位置右边，我们需要求rad值的位置
当前参考位置curL：在中心位置左边，我们已经求好了rad值的位置
我们发现有这样的几个等式：
- centerPos – curL = curR – centerPos
- centerL = 2*centerPos – curR
i-左回文串：中心距离centerPos i单位远的左侧的回文串，即以curL为中心的回文串
i-右回文串：中心距离centerPos i单位远的右侧的回文串，即以curR为中心的回文串
中心回文串：中心位置对应的回文串

深入问题

当我们处在中心位置centerPos的时候，我们之前已经求出了centerPos及之前所有位置的rad值了，这也意味着centerPos-d到centerPos+d是一个回文串。我们现在要处理curR位置，即算出rad[curR]。

我们需要一点分类讨论，首先是：

情形1:

i-左字符串被真包含（没有碰到中央回文串边界）于中心回文串内，且i-左字符串不是中心回文串的后缀，则有rad[curR] = rad[curL]，即：

C++

if (rad[curL] < centerR – curR){ rad[curR] = rad[curL]; }

1
2
3

if (rad[curL] < centerR – curR){
rad[curR] = rad[curL];
}

我们来考虑”abababa”这个例子：
manacher6

我们现在已经算出了rad[0~7]，中心位置 centerPos = 7，对应回文串半径 rad[centerPos] = d = 7，左边界 centerL = 0，右边界 centerR = 14。接下来我们要去算8及之后的rad值。

对于curR = 8，有curL = 6，和rad[curL] = 0，同时有 centerR – curR = 14 – 8 = 6，这符合情形1，所以我们有rad[curR] = rad[curL] = 0。

接下来对于curR = 10和curR = 12，也适用情形1。它们分别有：

rad[10] = rad[4] = 0
rad[1] = rad[2] = 0

然后，我们来看位置9，我们有：curR = 9， curL = 5，centerR – curR = 5。

这里我们有rad[curL] = centerR – curR，也就是说情形1并不适用。我们同时注意到了centerR是整个字符串的末尾，这也就意味着中心回文串是输入的字符串的后缀。也就是：

情形2:

当i-左回文串是中心回文串的前缀且中心回文串是输入字符串的后缀时，rad[curR] = rad[curL]。即：

C++

if ((rad[curL] == centerR – curR) && (centerR == 2*len(T))) rad[curR] = rad[curL]; //T是原始字符串

1
2
3

if ((rad[curL] == centerR – curR) && (centerR == 2*len(T)))
rad[curR] = rad[curL];
//T是原始字符串

位置9、11、13、14都适用情形2，我们有：

rad[0] = rad[5] = 5
rad[11] = rad[3] = 3
rad[13] = rad[1] = 1
rad[14] = rad[0] = 0

情形1和情形2的原理其实就是利用了回文串的性质，当一个较小的回文串被包含在一个较大的回文串中，且小回文串的中心在大回文串的左半部分时，根据回文串的对称性，大回文串应该有和左半部分相同的另外一个小回文串，中心在右半部分。

在情形1中，右边的回文串一定等于左边的回文串，否则如果右边的回文串能够扩张，左边的回文串也必然能够扩张，因为左边的回文串被真包含于大回文串之内（没有碰到大回文串边界），扩张时新加的字母也一定出现在了大回文串的右侧，扩张了右边的回文串，所以左边等于右边，反之亦然。

在情形2中，虽然左边的回文串是大回文串的前缀，如果右边发生扩张，不能保证对应的字母出现在左边，然而根据我们的条件，右边正好是整个输入字符的后缀，也就是右边的回文串根本不可能延长，所以左边等于右边。

上述的两种情形我们可以直接得出rad[curR]的值，不需要别的计算。

此外，还有两种情形：

情形3:

当i-左回文串是中心回文串的前缀且中心回文串不是输入字符串的后缀时，rad[curR] >= rad[curL]。即：

if ((rad[curL] == centerR – curR) && (centerR < 2*len(T))) { rad[curR] = rad[curL]; expand_required = true; } //T是原始字符串，expand_required标记表示接下来是不是要通过暴力计算来扩张curR。

1
2
3
4
5

if ((rad[curL] == centerR – curR) && (centerR < 2*len(T))) {
rad[curR] = rad[curL];
expand_required = true;
}
//T是原始字符串，expand_required标记表示接下来是不是要通过暴力计算来扩张curR。

情形3基于情形2，情形2的右边回文串是不能加字符扩张的，而情形3可以。当右边的回文串加字符扩张后，左边的回文串并不能扩张，因为新加的字符在中心回文串的外面，这个字符没有对应到左边去。

情形3只是给rad[curR]提供了一个下界，接下来我们需要暴力检验才能得到真实的rad[curR]，不过这依然减少了运算量。

情形4:

当i-左回文串与中心回文串交叉时，rad[curR] >= centerR – curR。即：

if (rad[curL] == centerR – curR) { rad[curR] = centerR - curR; expand_required = true; } //expand_required标记表示接下来是不是要通过暴力计算来扩张curR。

1
2
3
4
5

if (rad[curL] == centerR – curR) {
rad[curR] = centerR - curR;
expand_required = true;
}
//expand_required标记表示接下来是不是要通过暴力计算来扩张curR。

当我们的中心回文串不能覆盖左边回文串的时候，我们不妨缩小左边回文串到中心回文串能覆盖的程度，这样一来就和情形3是一样的了。

经过了以上四种情形的分类讨论，我们覆盖了所有在处理rad[curR]中可能出现的情况。

接下来我们基于这种思路来做实现。

实现

这份实现严格遵守了上面的思路，但是比较复杂，不太适合在实战中使用。

#define MANACHER_TUTORIAL
#ifdef MANACHER_TUTORIAL
namespace Manacher{
    const int MAXN = 1005;
    char str[MAXN];
    int rad[MAXN];//回文半径
    void manacher(){
        int len = strlen(str);
        len = (len << 1) + 1;
        rad[0] = 0,rad[1] = 1;

        int centerPos = 1;//当前回文串中心位置
        int centerR = 2;//当前回文串右边界
        int curR = 0;//当前正在处理的点(右部)
        int curL;//用于参考的点(左部)
        int maxLPS = 0,maxPOS = 0;
        int diff = -1,expand = -1;

        for(curR = 2;curR < len; curR++){
            //计算出参考点位置
            curL = 2*centerPos - curR;
            //重置扩张计数
            expand = 0;
            diff = centerR - curR;
            if(diff > 0){
                if(rad[curL] < diff){
                    //情形1
                    rad[curR] = rad[curL];
                }else if(rad[curL] == diff && curR == len-1){
                    //情形2
                    rad[curR] = rad[curL];
                }else if(rad[curL] == diff && curR < len-1){
                    //情形3
                    rad[curR] = rad[curL];
                    expand = 1;
                }else if(rad[curR] > diff){
                    //情形4
                    rad[curR] = diff;
                    expand = 1;//需要扩张curR为中心的回文串
                }
            }else{
                rad[curR] = 0;
                expand = 1;//需要扩张curR为中心的回文串
            }

            if(expand == 1){
                //尝试扩张以curR为中心的回文串
                //对于奇数的位置，需要比较字符是否相等来决定能否扩张
                //对于偶数的位置，直接扩张
                while(true){
                    if((curR + rad[curR] < len) && (curR - rad[curR] > 0));
                    else break;//达到了字符串边界，停止扩张
                    if((curR + rad[curR] + 1)&1)//奇数位置的情形:需要判断字符相等
                        if(str[(curR + rad[curR] + 1)/2] == str[(curR - rad[curR] - 1)/2])
                            rad[curR]++;
                        else break;//无法匹配字符，停止扩张
                        else rad[curR]++;//偶数位置的情形，直接扩张
                }
            }

            if(curR + rad[curR] > centerR){
                //如果curR对应的回文串扩张到了centerPos对应的回文串的外面
                //我们要移动centerPos到curR位置上，并算出新的右边界centerR
                centerPos = curR;
                centerR = curR + rad[curR];
            }
        }
    }
}

#endif

#define MANACHER_TUTORIAL

#ifdef MANACHER_TUTORIAL

namespace Manacher{

const int MAXN = 1005;

char str[MAXN];

int rad[MAXN];//回文半径

void manacher(){

int len = strlen(str);

len = (len << 1) + 1;

rad[0] = 0,rad[1] = 1;

int centerPos = 1;//当前回文串中心位置

int centerR = 2;//当前回文串右边界

int curR = 0;//当前正在处理的点(右部)

int curL;//用于参考的点(左部)

int maxLPS = 0,maxPOS = 0;

int diff = -1,expand = -1;

for(curR = 2;curR < len; curR++){

//计算出参考点位置

curL = 2*centerPos - curR;

//重置扩张计数

expand = 0;

diff = centerR - curR;

if(diff > 0){

if(rad[curL] < diff){

//情形1

rad[curR] = rad[curL];

}else if(rad[curL] == diff && curR == len-1){

//情形2

rad[curR] = rad[curL];

}else if(rad[curL] == diff && curR < len-1){

//情形3

rad[curR] = rad[curL];

expand = 1;

}else if(rad[curR] > diff){

//情形4

rad[curR] = diff;

expand = 1;//需要扩张curR为中心的回文串

}

}else{

rad[curR] = 0;

expand = 1;//需要扩张curR为中心的回文串

}

if(expand == 1){

//尝试扩张以curR为中心的回文串

//对于奇数的位置，需要比较字符是否相等来决定能否扩张

//对于偶数的位置，直接扩张

while(true){

if((curR + rad[curR] < len) && (curR - rad[curR] > 0));

else break;//达到了字符串边界，停止扩张

if((curR + rad[curR] + 1)&1)//奇数位置的情形:需要判断字符相等

if(str[(curR + rad[curR] + 1)/2] == str[(curR - rad[curR] - 1)/2])

rad[curR]++;

else break;//无法匹配字符，停止扩张

else rad[curR]++;//偶数位置的情形，直接扩张

}

if(curR + rad[curR] > centerR){

//如果curR对应的回文串扩张到了centerPos对应的回文串的外面

//我们要移动centerPos到curR位置上，并算出新的右边界centerR

centerPos = curR;

centerR = curR + rad[curR];

}

#endif

简化实现

观察一下我们分析的4种情形，我们会发现其实没有必要写那么繁琐，我们可以从下面几个方面减轻代码负担：

我们没必要计算S数组对应于T数组的位置，直接把S数组当作目标即可。
前3种情形都是令rad[curR] = rad[curL]，第四种情形是令rad[curR] = centerR – curR，我们不妨直接令rad[curR] = min(rad[curL], centerR – curR)。
对于情形1，2，不需要扩张，但我们尝试扩张也没什么关系。

这样，我们可以把上面的一大堆缩减到这样的程度：

#define MANACHER
#ifdef MANACHER
namespace Manacher{
    /*
     Manacher Algorithm.

     MAXN   : Maximum string length.
     rad    : Maximum panlidrome radius. <0,MAXN>
     tmp    : Alternated string for manacher working process. <0,2*MAXN>

     Example:
        hahaschool --> *#h#a#h#a#s#c#h#o#o#l#$ ($ being '\0')


     #define REP(i,t) for(int i = 0;i < t; i++)
     #define REP_1(i,t) for(int i = 1;i <= t; i++)

     Time   : O(n)
     Space  : 3n
     */
    const int MAXN = 1005;
    char tmp[MAXN*2];
    int rad[MAXN];
    void manacher(char *str){
        memset(tmp, 0, sizeof(tmp));
        //将原始字符串插入辅助字符(必须确保下述两个辅助字符没有在字符串中出现过)
        tmp[0] = '*', tmp[1] = '#';
        int len = strlen(str);
        REP(i, len){
            tmp[i*2+2] = str[i];
            tmp[i*2+3] = '#';
        }
        len = (len+1)<<1;
        tmp[len] = 0;

        //Manacher主过程
        //id:当前回文串中心 ma:当前回文串右边界
        int id = 0,ma = 0;
        REP_1(i, len-1){//正在处理的右部点
            if(ma > i) rad[i] = min(ma-i,rad[id*2-i]);//拉取当前回文串的"基本长度"
            else rad[i] = 1;//当前处理中心已经超出右边界，只能暴力扩张
            while(tmp[i-rad[i]] == tmp[i+rad[i]]) rad[i]++;//尝试扩张以i为中心的回文串
            if(i + rad[i] > ma){//当以i为中心的回文串超出右边界，要更改中心点和算出新的右边界
                id = i;
                ma = i + rad[i];
            }
        }
    }
}

#endif

#define MANACHER

#ifdef MANACHER

namespace Manacher{

Manacher Algorithm.

MAXN : Maximum string length.

rad : Maximum panlidrome radius. <0,MAXN>

tmp : Alternated string for manacher working process. <0,2*MAXN>

Example:

hahaschool --> *#h#a#h#a#s#c#h#o#o#l#$ ($ being '\0')

#define REP(i,t) for(int i = 0;i < t; i++)

#define REP_1(i,t) for(int i = 1;i <= t; i++)

Time : O(n)

Space : 3n

const int MAXN = 1005;

char tmp[MAXN*2];

int rad[MAXN];

void manacher(char *str){

memset(tmp, 0, sizeof(tmp));

//将原始字符串插入辅助字符(必须确保下述两个辅助字符没有在字符串中出现过)

tmp[0] = '*', tmp[1] = '#';

int len = strlen(str);

REP(i, len){

tmp[i*2+2] = str[i];

tmp[i*2+3] = '#';

}

len = (len+1)<<1;

tmp[len] = 0;

//Manacher主过程

//id:当前回文串中心 ma:当前回文串右边界

int id = 0,ma = 0;

REP_1(i, len-1){//正在处理的右部点

if(ma > i) rad[i] = min(ma-i,rad[id*2-i]);//拉取当前回文串的"基本长度"

else rad[i] = 1;//当前处理中心已经超出右边界，只能暴力扩张

while(tmp[i-rad[i]] == tmp[i+rad[i]]) rad[i]++;//尝试扩张以i为中心的回文串

if(i + rad[i] > ma){//当以i为中心的回文串超出右边界，要更改中心点和算出新的右边界

id = i;

ma = i + rad[i];

}

#endif

不刻意压行就可以达到简短的20行代码，非常简洁好记。

应用举例

裸题

左端点对应最长回文串

结合线段树

参考文献与致谢

Anurag Singh from GeeksforGeeks for pictures and some ideas.
doubility::Zhenkun Csi for beautiful implementation in C++.

给中级者的动态规划教程

January 21, 20162016-01-21hahaschoolLeave a comment

认识更多模型

区间DP

POJ 2955 Brackets：最简单的区间DP，括号序列

LA4394 String Painter：两层区间DP，难度较大

概率DP

POJ 3744 Scout YYF I：概率型递推配合矩阵快速幂加速

POJ 2096 Collecting Bugs：优惠券问题的二维情形

状态压缩DP

UVA 10911 Forming Quiz Teams：最优配对问题

LA3725 Hie with the Pie：TSP问题

树DP

POJ 1655 Balancing Act：求树的重心

Codeforces 461B Appleman and Tree：最大独立集问题的变种

LA4394 String Painter

January 21, 20162016-01-21hahaschoolLeave a comment

题意

给定两个长度相等，只有小写字母构成的字符串s和t，每步可以把s的一个连续子串“刷”成同一个字母，问至少多少步才能把s变成t。

思路

两层区间DP。

首先忽略原始串s，只去看目标串t，设dp1[i][j]表示从什么都没有的情况下利用刷子规则构造出目标串t的i到j这一段所需要的最小操作次数。这里着眼于“最后一次操作”进行阶段的划分。

dp1的状态转移：

dp[i][j] = dp[i+1][j ] + 1
先默认最后一次操作是只刷出最新那个字符。
令k是i和j中间的某个位置，t是目标串，如果t[i] == t[k]
尝试用dp[i+1][k] + dp[k+1][j]更新dp[i][j]
因为i处字符等于k处字符，在构造i+1到k这个区段的时候，可以在刷k处字符的同时“顺便”把i位置也给刷了。
注意这里不可以写成dp[i+1][k-1] + 1 + dp[k+1][j]，考虑反例” /e(i对应)/ee/e(k对应)/… “,在这里dp[i+1][k-1]是1，用这种错误的算法dp[i][k]部分会变成2，但实际上应该是1。

接下来引入原始串s，令dp2[i]表示把原始串1到i构造成目标串1到i的部分所需要的最小的操作次数。这里有状态转移：

默认dp2 = dp1[1][i]
如果s[i] == t[i]
尝试dp2[i] = dp2[i-1]
否则尝试dp2[i] = dp2[i-1] + 1

这里的意思是如果在第i位两个串对应字符相等，可以选择无需对这一位进行操作
令k是1到i之间的位置
尝试dp2[i] = dp2[k-1] + dp1[k][j]

这里的意思是假设最后k位使用不考虑原始状态的构造方法，前面继承最优解。为什么要这样做？考虑fabcf这样的区间，一种较好的策略是先都刷成f，然后分别刷好abc，如果你选择这么做了，相当于已经无视了原来串的样子，因为第一步已经将全部中间字符都刷成f了。

代码

#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <string>
#include <cstring>
#include <ctime>
#include <iomanip>
#include <cmath>
#include <set>
#include <stack>
#include <cmath>

using namespace std;

int dp[105][105];
int res[105];

int main(){
    string a,b;
    while(cin >> a >> b){
        memset(dp,0,sizeof(dp));
        memset(res,0,sizeof(res));
        int n = (int)a.size();
        for(int i = 1;i <= n;i++){
            dp[i][i] = 1;
        }
        for(int i = n-1;i >= 1;i--){
            for(int j = i+1;j <= n;j++){
                dp[i][j] = dp[i+1][j] + 1;
                for(int k = i+1;k <= j;k++){
                    if(b[i-1] == b[k-1]){
                        dp[i][j] = min(dp[i][j],dp[i+1][k]+dp[k+1][j]);
                    }

                }
            }
        }
        for(int i = 1;i <= n ;i++){
            res[i] = min(dp[1][i],res[i-1]+(a[i-1] != b[i-1]));
            for(int j = 1;j <= i;j++){
                res[i] = min(res[i],res[j]+dp[j+1][i]);
            }
        }
        cout << res[n] << endl;
    }
    return 0;
}

#include <iostream>

#include <algorithm>

#include <queue>

#include <vector>

#include <cstdlib>

#include <cstdio>

#include <string>

#include <cstring>

#include <ctime>

#include <iomanip>

#include <cmath>

#include <set>

#include <stack>

#include <cmath>

using namespace std;

int dp[105][105];

int res[105];

int main(){

string a,b;

while(cin >> a >> b){

memset(dp,0,sizeof(dp));

memset(res,0,sizeof(res));

int n = (int)a.size();

for(int i = 1;i <= n;i++){

dp[i][i] = 1;

}

for(int i = n-1;i >= 1;i--){

for(int j = i+1;j <= n;j++){

dp[i][j] = dp[i+1][j] + 1;

for(int k = i+1;k <= j;k++){

if(b[i-1] == b[k-1]){

dp[i][j] = min(dp[i][j],dp[i+1][k]+dp[k+1][j]);

}

for(int i = 1;i <= n ;i++){

res[i] = min(dp[1][i],res[i-1]+(a[i-1] != b[i-1]));

for(int j = 1;j <= i;j++){

res[i] = min(res[i],res[j]+dp[j+1][i]);

}

cout << res[n] << endl;

}

return 0;

}

LA3725 Hie with the Pie

January 21, 20162016-01-21hahaschoolLeave a comment

题意

经典问题：TSP。

给出了n个城市，求一条最短的路径，使得经过每个城市一次且仅一次，最后回到起点。

思路

状态压缩DP。分析问题可知道是一个多阶段决策过程，每个阶段“状态”包括了可以用已经走了哪些点，和当前站在哪个点，决策就是接下来走哪个点。

状态表示：dp[二进制位，表示目前已经走过那些点][最后走的点的序号] = 从起点出发走过的最短路程

答案：min{dp[走过全部点的状态][枚举各个可能的最后走的点i] + dis(i,起点)}

边界：dp[0][起点] = 0,其它都是INF

状态转移：用dp[S][i] + dis(i,j) 去尝试更新dp[S|j][j]

代码

#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <string>
#include <cstring>
#include <ctime>
#include <iomanip>
#include <cmath>
#include <set>
#include <stack>
#include <cmath>
#include <map>

using namespace std;

int n;
long long dis[12][12];
long long dp[12][4096];

void floyd_warshall(){
    for (int k = 0; k <=n;k++) {
        for(int i = 0; i<= n; i++){
            for(int j = 0; j<=n ;j++){
                if(dis[i][k] + dis[k][j] < dis[i][j]){
                    dis[i][j] = dis[i][k] + dis[k][j];
                }
            }
        }
    }
}

long long solve(){
    memset(dp, 0x3f, sizeof(dp));
    for(int i = 0; i < (1 << n) ;i++){
        int cnt = 0,lst = 0;
        for(int j = 1; j <= n; j++){
            if(i & (1 << (j-1))){
                cnt++;
                lst = j;
            }
        }
        if(cnt <= 1){
            dp[lst][i] = dis[0][lst];
        }else{
            for(int j = 1; j <= n; j++){
                if(i & (1 << (j-1))){
                    for(int k = 1; k <= n; k++){
                        if(j != k && i & (1 << (k-1))){
                            dp[j][i] = min(dp[j][i],dp[k][i^(1 << (j-1))] + dis[k][j]);
                        }
                    }
                }
            }
        }
    }
    long long ret = 0x3f3f3f3f3f3f3f3f;
    for(int i = 1; i<=n;i++){
        ret = min(ret,dp[i][(1 << n)-1] + dis[i][0]);
    }
    return ret;
}

int main(){
    //freopen("testdata.in", "r", stdin);
    while(scanf(" %d",&n) != EOF && n){
        for(int i = 0; i <= n ;i++){
            for(int j =0;j <= n; j++){
                scanf(" %lld",&dis[i][j]);
            }
        }
        floyd_warshall();
        printf("%lld\n",solve());
    }

    return 0;
}

#include <iostream>

#include <algorithm>

#include <queue>

#include <vector>

#include <cstdlib>

#include <cstdio>

#include <string>

#include <cstring>

#include <ctime>

#include <iomanip>

#include <cmath>

#include <set>

#include <stack>

#include <cmath>

#include <map>

using namespace std;

int n;

long long dis[12][12];

long long dp[12][4096];

void floyd_warshall(){

for (int k = 0; k <=n;k++) {

for(int i = 0; i<= n; i++){

for(int j = 0; j<=n ;j++){

if(dis[i][k] + dis[k][j] < dis[i][j]){

dis[i][j] = dis[i][k] + dis[k][j];

}

long long solve(){

memset(dp, 0x3f, sizeof(dp));

for(int i = 0; i < (1 << n) ;i++){

int cnt = 0,lst = 0;

for(int j = 1; j <= n; j++){

if(i & (1 << (j-1))){

cnt++;

lst = j;

}

if(cnt <= 1){

dp[lst][i] = dis[0][lst];

}else{

for(int j = 1; j <= n; j++){

if(i & (1 << (j-1))){

for(int k = 1; k <= n; k++){

if(j != k && i & (1 << (k-1))){

dp[j][i] = min(dp[j][i],dp[k][i^(1 << (j-1))] + dis[k][j]);

}

long long ret = 0x3f3f3f3f3f3f3f3f;

for(int i = 1; i<=n;i++){

ret = min(ret,dp[i][(1 << n)-1] + dis[i][0]);

}

return ret;

}

int main(){

//freopen("testdata.in", "r", stdin);

while(scanf(" %d",&n) != EOF && n){

for(int i = 0; i <= n ;i++){

for(int j =0;j <= n; j++){

scanf(" %lld",&dis[i][j]);

}

floyd_warshall();

printf("%lld\n",solve());

}

return 0;

}

UVA 10911 Forming Quiz Teams

January 21, 20162016-01-21hahaschoolLeave a comment

题意

经典模型“最优配对问题”，给出了平面上若干个点，你要把牠们两两配对，使得每一对中两点距离之和最小。

思路

分析问题：我们发现，本问题可以着眼于“最后一次配对”，是一个多阶段决策。不妨考虑当最后一次选择拿i号点去和j号点去配对,得到了某种状态时可以得到的最优解。

状态表示：dp[当前状态下各个点是否已经配对][最后一次配对的点i][最后一次配对的点j]

我们发现这个状态设的太繁了，假如我们要配对a和b这两个点，那么在所有的配对状态里面都要算入a和b的距离，在所有没配对状态里都不可以算入a和b的距离，后两个维度强行决定了一组点的配对情况，然而并没有什么意义，因为后两个维度的信息已经包括进了第一个维度里，我们只要想办法让第一个维度可以表达出决策的“分阶段”特性，能够识别出最后一步是什么就可以。

于是我们重设状态：dp[当前状态下各个点是否已经配对]并且规定在每个状态中，最低位为1对应的那个点是我们最后一次操作的点。

这样有状态转移：dp[S] = min{dis(i,j) + dp[S^i^j]} 在这里S是二进制表示的状态，i,j是假定的最后一次配对的点对，其中规定i一定是S中最低位的那个点，dis表示求距离，S^i^j表示将二进制表示的状态中i,j对应的位设成零之后得到的二进制状态

代码

#include <iostream>
#include <cstdio>

using namespace std;

int n;
struct Student{
    double x;
    double y;
    string name;
} stu[17];

double dis(Student &a,Student &b){
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

double dp[17][100000];

double solve(){
    memset(dp, 0x77, sizeof(dp));
    dp[0][0] = 0;
    dp[1][0] = 0;
    dp[1][1] = 0;
    for(int i = 2;i <= n; i++){
        for(int j = 0; j < (1 << i) ;j++){
            if(j&(1 << (i-1))){
                for(int k = 1; k < i; k++){
                    if(j & (1 << (k-1))){
                        dp[i][j] = min(dp[i][j],dp[i-1][j^(1 << (i-1))^(1 << (k-1))] + dis(stu[i], stu[k]));
                    }
                }
            }else{
                dp[i][j] = dp[i-1][j];
            }

        }
    }
    return dp[n][(1 << n)-1];
}

int main(){
    int caseCnt = 0;
    while(cin >> n){
        if(!n){
            break;
        }
        n *= 2;
        caseCnt++;
        for(int i = 1; i <= n; i++){
            cin >> stu[i].name >> stu[i].x >> stu[i].y;
        }
        cout << "Case " << caseCnt << ": "  << fixed << setprecision(2) << solve() << endl;
    }

    return 0;
}

#include <iostream>

#include <cstdio>

using namespace std;

int n;

struct Student{

double x;

double y;

string name;

} stu[17];

double dis(Student &a,Student &b){

return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));

}

double dp[17][100000];

double solve(){

memset(dp, 0x77, sizeof(dp));

dp[0][0] = 0;

dp[1][0] = 0;

dp[1][1] = 0;

for(int i = 2;i <= n; i++){

for(int j = 0; j < (1 << i) ;j++){

if(j&(1 << (i-1))){

for(int k = 1; k < i; k++){

if(j & (1 << (k-1))){

dp[i][j] = min(dp[i][j],dp[i-1][j^(1 << (i-1))^(1 << (k-1))] + dis(stu[i], stu[k]));

}

}else{

dp[i][j] = dp[i-1][j];

}

return dp[n][(1 << n)-1];

}

int main(){

int caseCnt = 0;

while(cin >> n){

if(!n){

break;

}

n *= 2;

caseCnt++;

for(int i = 1; i <= n; i++){

cin >> stu[i].name >> stu[i].x >> stu[i].y;

}

cout << "Case " << caseCnt << ": " << fixed << setprecision(2) << solve() << endl;

}

return 0;

}