[toc]
图(Graph)作为一种非常常见且有效的模型和抽象手段,不仅是在竞赛中,乃至整个CS的学习和应用过程中都有着举足轻重的地位,尽早掌握一些关于图的概念也能辅助我们更好地分析手边的问题。本文介绍一些关于图的最基本概念和实际应用上的一些基本技术。
图的基本知识
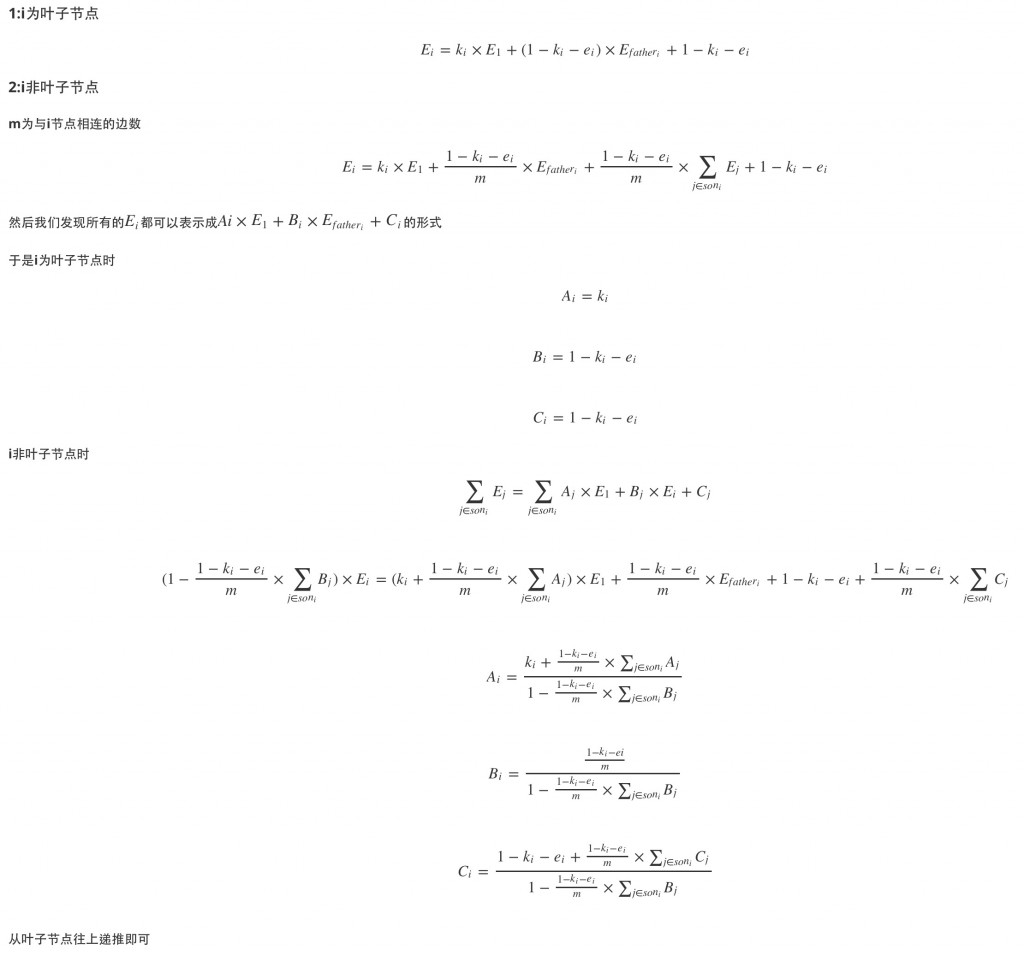
在这里我给出这样一个问题:你站在1上,1能走到3,1能走到2也能从2走回来,7能走到5也能从5走回来,7能走到6也能从6走回来,2和5和6互相连通,1自己能走到自己,3能走到4.那么你都能走到那些点呢?
你可能很自然的会想到把我上面说的那一坨给画成一个“路线图”或“地图”,这样只要一看这个图就可以一目了然了,而接下来要说的计算机/数学中的“图”就是这样的一种抽象方式。
来和“图”桑见一面
图的定义很简单,给你几个圆,再把圆和圆之间拿线连起来,就可以称为图了。
定义: 由若干个不同的顶点与连接其中某些顶点的边组成的图形称为图。
 An Example of Graph
An Example of Graph
上面这个就是一个典型的图了,这个图反映的就是我上文中说的那些关系,图里绿色的圆,称为“节点/顶点(Node/Vertex)“,为了接下来叙述的方便,我给每一个节点都挂上了一个编号,在实际应用中,节点上能够挂载任何你需要的信息。圆与圆之间连接着的线,不管长成什么样,都称为“边(Edge)”,边上面也可以挂载信息。
我们发现了,上图中边中,有的是拿直线段表示的,这种边称为“无向边”,比如上面图中的2号点和5号点的连边,这样的边表示“一端(2号点)和另外一端(5号点)可以经由此边互相到达”。‘
而3号点和4号点之间的连边上面有一个箭头,方向是3号到4号,这样的边称为“有向边”,含义是“你只能从一端(3号)经由此边到达另一端(4号),但是并不能反过来”。这样看来,其实无向边可以看成两条方向互反的有向边,这一条性质非常有用。
有的时候,在两个节点之间,可能有着多条无向边或者是相同方向的有向边,这种情况,称为“重边”。
然后再看1号点,我们发现他自己居然和自己连了一条边,这样的边称为“自环”。
而看一下2号、5号、6号和7号,我们发现这四个节点,和他们之间的边共同组成了一个“环”,如果我们以一个方向沿着环行走,恐怕是一辈子也出不去了-_-#。组成环的边可以是无向的,也可以是有向的,沿着一系列的有向边行走,最后走回到了起点,这些有向边就组成了“有向环”。
给图挂载信息
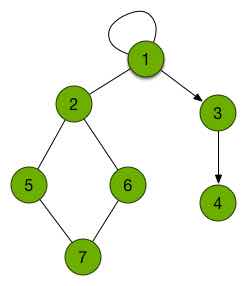
我们先假设这样一种问题情境:你自驾去了一个旅游区,现在正在景区门口盘算着旅游的路线,你知道景区里面没办法加油,所以你已经加满油了,你的油箱容量是K个单位,现在给了你景区的平面图,上面记载了两个景点之间连接着的最近道路的距离(已经被折算成了通过一次要消耗的油量)和你来景区之前调查好的每一个景点的美丽程度。你需要设计一种路线,使得可以用有限的K个单位的燃料,游玩的景点的美丽程度之和最大(你不用考虑游玩结束没油怎么回景区的问题,因为你的保险公司提供免费的拖车服务)。
这个问题就是图论派上用场的时候了,我在这里随便举了一组实例:
景区大门和每一个景点,都可以抽象为图上的一个顶点,而每一条道路都可以抽象为图上的一条边。
我们知道每一个景点都有一个“美丽程度”,这个美丽程度就体现在上面这个图里面每一个节点里填着的数字,我们把这种称为“点权”。
每一条道路,都有一个“耗油量”,体现在图上就是边上的数字就是“边权”。
所谓“权(Weight)”,其实就是一种定量的评价标准,怎么样理解附挂在图上的权,是我们自己决定的。
而图上附挂的信息又不仅仅是权值,理论上我们可以给图的任何部分挂载任何我们想要的信息,试想一下,如果我们给每一个节点挂载一个列表,上边记载了从这个可以到达的全部节点的编号,会怎么样?如果我们给每一条边挂载一个数对,上面记载了边的两端所连接的节点的序号,会怎么样?
而接下来要讲的“图的存储”,其实就是几种“挂载信息”的方式。
图的常见存储方式
计算机是不长眼睛的,你也不可能指望它看到上面我们画出来的圆和线就能解决问题。因此我们要把手中的图通过一种计算机可以理解的方式进行转化并存储才行。
常见的存储方式有四种:“邻接矩阵”、“邻接表”、“前向星”、“链式前向星”。他们各有各的特点,其中“前向星”和“链式前向星”其实是邻接表的实现方式,这两种里面我们只需要学习“链式前向星”就可以了。
邻接矩阵
首先,为了方便起见,我们要把图中每一个节点都编号,在这里我们编号1~n。接下来创建一个n*n的全是0的矩阵(或者其他你设定的用来表示无法联通的值),然后我们挨个处理图中的每一条边,对于一条有向边,从a号点指向b号点,那么我们就把矩阵的a行b列修改为1,表示从a到b可以通过。对于一条无向边,连通着a号点和b号点,那么我们就把矩阵的a行b列、b行a列都修改为1,因为无向边可以看成两条方向互反的有向边。
|
|
int graph_mat[MAXN][MAXN]; void graph_init(){ memset(graph_mat, 0, sizeof(graph_mat)); } void graph_add_edge(int from,int to){ graph_mat[from][to] = 1; } |
如果你想给边挂边权,怎么办?很简单,矩阵的数值就可以当成边权来用,不过如果你的权值和矩阵中你设定的标记冲突,你就要单独开一个数组来记录了。
如果你想给点挂点权,也需要单独开一个数组来记录。
邻接矩阵的特点是查询一个点到另外一个点之间是否有边和这条边的信息,O(1)就可以查到。但是如果我们要询问一个点连出/连入的所有边(也就是所谓的“遍历”),就必须要检查邻接矩阵的一整行/一整列,这样复杂度就是O(n)。同时,因为是使用数组保存,如果图里有重边,你最终只能保存最后保存的那一条边,也就是会丢失信息,因此一旦有无法忽略的重边,就一定不可以使用邻接矩阵。
看到这里你可能觉得邻接矩阵有点傻,那你可就错了。求多源最短路的Floyd-Warshall算法,求传递闭包的Floyd-Warshall算法,有限状态自动机的状态转移方法数等等都是要使用邻接矩阵的。
邻接表(STL vector实现)
还记得上文的“如果我们给每一个节点挂载一个列表,上边记载了从这个可以到达的全部节点的编号,会怎么样”吗?其实这就是邻接表的一种实现方式。
我们依然要给每一个节点编号,不过这时更多的是为了方便了(如果不编号,就可能要借助指针)。对于每一个点,我们给它挂上一个vector,在这里我给他起名叫to。然后我们还是挨个处理原图中的每一条边。对于一条从a到b的有向边,我们只要对a中的to.push_back(b)就可以了。对于无向边,因为无向边可以看成两条方向互反的有向边,所以就是a.to.push_back(b)和b.to.push_back(a)两步。
|
|
struct Node { vector<int> to; } vertex[MAXN]; void graph_init(int n){ for (int i = 1; i <= n; i++) { vertex[i].to.clear(); } } void graph_add_edge(int from,int to){ vertex[from].to.push_back(to); } |
在这里我用了个结构体,这是为了方便我们挂载信息的。如果我们想挂点权,直接在Node里面多来一个int什么的就好,如果想挂边权,就再来一个vector,与to同步push_back对应边的权值。
邻接表非常常用,首先他是以点为主体,边是作为点的信息存在的,这一点很符合我们的思考规律。其次因为边采用vector保存,所以不用担心重边丢失的问题。邻接表逊色于邻接矩阵的地方恐怕就只有查询两个点之间是否有边了,在邻接表里面你必须遍历整个当前点上的to才能判断是不是能和另外一个点相连。但相对的,如果图中的点连接的边不多的话(这时候的图可以称为“疏松图”,反之,“稠密图”),邻接矩阵下的O(n)的遍历在邻接表下就快多了。
链式前向星(静态建表的邻接表实现)
上文中我们还提到了“如果我们给每一条边挂载一个数对,上面记载了边的两端所连接的节点的序号,会怎么样?”,其实链式前向星就是这种思路。
在这里假定你已经很明白链表的工作方式了,链式前向星其实就是图上所有边按照某种特殊的方式组成的链表。因为比较难理解,我先上代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
struct Graph{ int head[MAXN]; int next[MAXN]; int to[MAXN]; inline void addEdge(int _from,int _to){ static int q = 1; to[q] = _to; next[q] = head[_from]; head[_from] = q++; } } graph; void iteration(){//遍历的方法 int now;//now 是当前所处的节点标号 for (int j = idx.head[now]; j; j = idx.next[j]) { //operate node j,j是now所连接着的节点编号 } } |
使用上,还是先编号,然后挨个边处理,直接调用addEdge()方法就可以,查询一个节点所连出的边是,使用上面代码里iteration()里的方法,利用一个略微奇怪的for循环就可以办到。
我们不妨直接从代码的实现来分析链式前向星的工作原理,结构体里面的head是每一个节点在容器(数组)中所对应的第一条边的位置,next是每一条边在容器中所对应的同一起点的下一条边的位置,to则是真正的存储某一条边是指向哪一点的。
再看加边操作,注意到方法里的q是静态变量,这一点非常重要,q的作用是指示当前存储边的容器的末端(注意“末端”指的是并不是最后一个元素,而是其后的空地)的位置,相当于STL迭代器的end(),每一次加边的时候,要在to的末端写入新加边的信息,然后通过head[_from]提取出起点最近加的一条边的位置,然后我们要把新加的边的next指向那一条边,最后修改head,使得最近添加的边变更为新边,同时末端向后移动以供下一次添加之用。
理解了这样的加边方法,查询一个点连出的边的方法也就很好理解,要查询一个点的连出边,我们要先查head,知道这个点最近添加的那条边在哪里(查询结果在这里是j),然后比这条边早一些添加的就是next[j],再早一点的就是next[next[j]],更早一点的是next[next[next[j]]],再早一点的是……,就这样我们一直往时间添加时间更早的边查,直到查到空节点(用来标记链表结束)。
可以发现,链式前向星相对于邻接表的vector实现,常数更小。同时如果想直接遍历每一条边,而不考虑顺序,可以直接遍历to数组(当然,为了知道每条边的起点,你可能还需要建一个from数组),这就使得我们可以从边入手解决问题。因为是邻接表,我们也可以以点为中心来考虑问题。基本可以说链式前向星在各方面都优于邻接表的vector实现。
如果你不用数组,而是用指针来实现,那就是“前向星”了。
暴力搜索
树
在讲搜索之前,我们还要再来一点关于图的话题,那就是“树”,当然不是种出来的树,而是一种特别一点的图,不过就像你在大街上看到的各种树一样,能被称为一棵“树”的图一定要满足以下几种特征:
- 每两个点之间有且仅有一条路径
- 没有环,而且只要再添加一条边,就一定会出现环
- 只要去掉一条边,就无法保证第一条性质
- 只要增加一个点,为了保证第一条性质就必须还要增加一条边
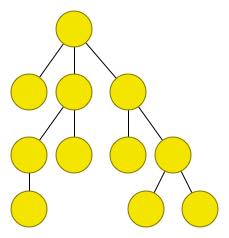 An Example of Tree
An Example of Tree
如果只有光秃秃的一个节点,其实也可以称为树,树上的边的方向性也没有要求,可以有向也可以无向,当有多棵“树”同时存在的时候,这些互相没有相交的树共同组成的图也被称作“森林”。
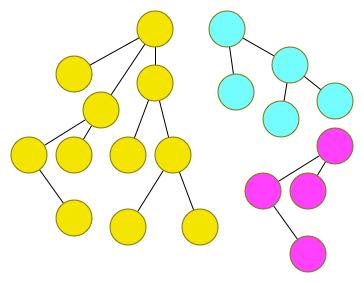 An Example of Forest
An Example of Forest
自然界的树都是有根的,同样的,有时候为了分析问题的便利,我们也会选取树上的某个节点作为“根节点”。选取了根节点的树这时候也称为“有根树”。
选取了根之后,伴随之而来的还有节点与节点之间的“辈分关系”,我们把根视为辈分最大的祖先,他连接的所有点都是它的“孩子”,而对于他连接着的所有点来说他就是这些点的“父亲”。这样的关系对于所有的节点都是一样的,我们注意到了,在一棵树上,每个节点可以有好多孩子,但是只能有一个父亲,而对于没有孩子的节点,我们对他还有一个称呼叫“叶子节点”,对于有同一个父亲的若干个节点,他们互称“兄弟节点”。
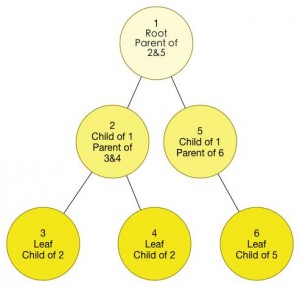 Relation on a Tree
Relation on a Tree
细心的你也发现了,上面这幅图从上面到下面颜色是越来越深的,没错,我想借此来表达有根树的“深度”概念。对于根部,他的“辈分”最大,但是他的“深度”是最小的,父亲的深度始终是比孩子节点的深度大1的。
理解了上面的这些概念,我们就可以开始说“暴力搜索”了。
我们说的“搜索”是什么
我们对搜索的认识,恐怕都是来源于“百度”、“谷歌”,也就是“从所有的信息中找出我们需要的信息的这一过程”,而我们现在接下来要说的“搜索”虽然感觉上还是和你键入几个关键字然后敲回车有一定区别的,但是实质上其实是一样的,不过现在这个过程要交给你亲自去实现。
试想这么几个问题,给你一个表示各个景点之间连通关系的图,现在让你找13号点在哪里,你如何“系统地”完成这个寻找过程?给你一个迷宫,里面有好多墙壁,现在要你找出脱出迷宫的最短路线,你又该如何“系统地”完成这一过程?更直接地,给你一棵树,制定一个根部,你能“系统地”把这棵树的亲子关系和深度都算出来吗?
这些问题,对于你来说可能就是瞟一眼那样简单,不过你知道计算机可是没有眼睛的,也没法扫视全局,因此“系统性”的算法就显得非常重要,也就是说你要有一种“套路”,而不是随便去瞟一眼这么简单。
接下来我们要介绍两种最为常见的搜索“套路”,深度优先搜索和广度优先搜索。在学习这些之前,我已经假定你理解了我上面所讲的图,树的概念,以及栈,递归(调用栈),队列的知识。
深度优先搜索(Depth First Search)
理解深度优先搜索(DFS)的最佳途径就是从“树的先序遍历(DLR)”开始,所谓“遍历”就是把树的每一个节点都走一遍。树的先序遍历,是指对于给定的一棵有根树,从这棵树的根部开始,不断尝试进入儿子节点(下潜),直到进入了叶子节点,然后才会返回到上一层,继续查找下一个儿子节点进入,通过不断重复这一过程,直到所有的节点都被进入并最终返回根部。简单的说就是:不断尝试探底,不走重复的路。下面举个例子来解说:
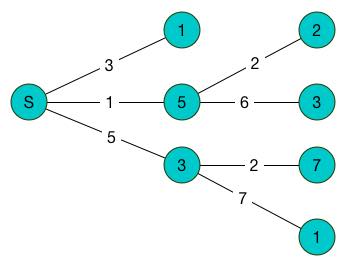
在这里我给出了一棵树,并且设定好了根部,同时因为我们的起点在根部,我把根部标记为1.
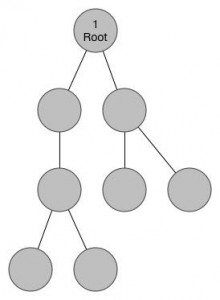 Example Tree to Show DLR
Example Tree to Show DLR
根节点(1号节点),连接了两个儿子节点,按照上文所述的思想,我们优先访问最左面的那个,我们把它标记为2,并进入这个节点。
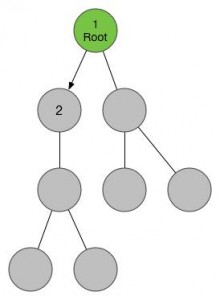
进入2号节点之后,我们顺着刚才的思路,不断下潜,最后我们到达了叶子节点4号。
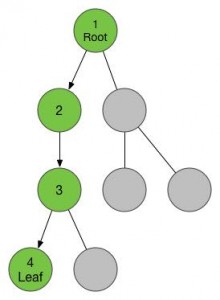
现在我们发现没有可以用的孩子节点了,那么我们就要回到当前节点的父亲那里去,也就是3号节点。在3号节点,我们发现了除了已访问的4号节点之外的另外一个儿子,我们把它标记为5号节点,并进入。
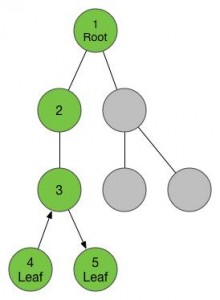
我们在5号节点又遇到了4号一样的情况,没有儿子,那样的话我们就要返回父亲节点3号。当我们返回3号,我们发现儿子已经走了个遍了,这个时候我们又要返回父亲节点2号,在2号同样没有可以没走过的儿子了,我们返回到2号的父亲节点1号。
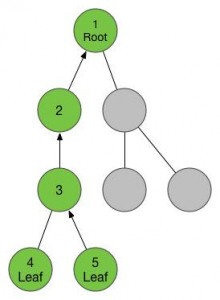
等我们回到了一号节点,我们又可以找到新的没有走过的儿子了,于是我们按照刚才的调子,进入这个儿子,这个节点已经是我们走过的第6个新节点了,给他标号6,然后我们又找到了他的儿子,进入,标号7。
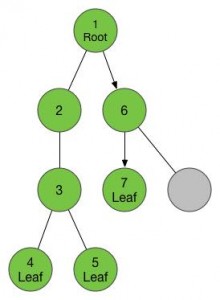
7号节点又是叶子节点,于是我们返回到他的父亲6号,然后发现还有一个没走过的儿子,于是进入,标号8。
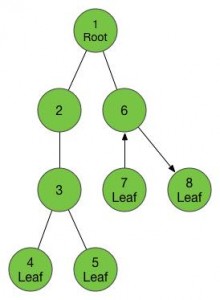
8是叶子节点,返回6,6没有没走过的儿子,返回1,1没有没走过的儿子。好了,任务完成了!
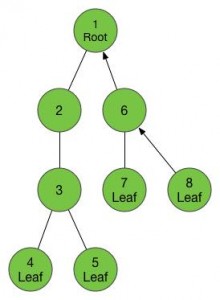
以上就是“树的先序遍历”,是不是很简单?而DFS其实就可以理解成先序遍历在各种其他情境的推广,比如各种“图的遍历”、迷宫搜索(可以转化为图)、找出联通块(水洼问题)等等。通过思考我们也发现了,DFS实现起来的最佳方式就是递归,递归可以完美的还原我们的“下潜(发动递归)”和“返回(函数返回)”动作。下面我给出使用DFS遍历图的实现,使用了vector邻接表,所有访问到的节点,均会在标记数组vis中被标true。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
struct Node{ vector<int> to; } vertex[1000]; void addEdge(int from,int to){ vertex[from].to.push_back(to); } bool vis[1000]; void dfs(int cur){ vis[cur] = true; for (int i = 0; i < vertex[cur].to.size(); i++) { if (!vis[vertex[cur].to[i]]) { dfs(vertex[cur].to[i]); } } } |
如果你还是一头雾水,不妨试着将上面我做演示的那棵树建立成图,然后手动模拟一边这份实现的执行过程,就能理解了(前提是你必须知道递归和栈的原理)。
一旦你发动了dfs(a),那么在搜索执行完毕之后,所有与a号节点直接或间接连通的点都会被在vis中标记,所以只要对这份实现稍加改动,我们就可以解决“水洼问题”了。而要想解决“迷宫出路”这种问题,我们还要稍微动下脑筋,思考一下vis这个标记数组应该怎样活用,怎样利用vis让dfs达到我们想要的效果(在这份实现中,一旦一条路被走过,就无法再次走过,而在迷宫中,我们很有可能要走之前走过的道路,这样我们就要适时地复原vis标记)。
广度优先搜索(Breadth First Search)
相对于DFS,广度优先搜索(BFS)也许更加直观一点,我们还是从“树的遍历”说起。对于一棵给定的有根树,我们依然从根开始入手,不过这次我们建立了一个队列,队列存储的是“状态”,最开始队列是空的,要开始搜索,我们要给他加入“当前在根节点”这一状态,之后我们不断拉取队伍的队首,然后分别把我们进入了各个儿子的状态逐一加入队列,直到队列清空,这个时候我们一定把每一个“在XX节点”的状态都经历过了,所以我们是走遍了整棵树。
我在这里依然用在DFS里的那棵树来举例子,图下面的方括号,表示队列的变化,左半方括号表示队列头,右半方括号表示队列尾。
最开始,我们的队列里只有1号状态,我们给它拿出来,然后发现他有两个儿子,于是分别创建进入2号儿子的2号状态和进入3号儿子的3号状态,并将他们加入队列尾端。
 [1] -> [2,3]接下来,我们取出队列头的2号状态,我们发现它只有一个儿子,我给他标号4,于是把“进入4号节点”的4号状态加入队列。
[1] -> [2,3]接下来,我们取出队列头的2号状态,我们发现它只有一个儿子,我给他标号4,于是把“进入4号节点”的4号状态加入队列。
![[2,3] -> [3,4]](https://haha.school/wp-content/uploads/2015/09/g141.jpeg) [2,3] -> [3,4]接下来,取出队列头的3号状态,我们发现它有两个儿子,在这里标号为5和6,于是借此生成5号和6号状态,加入队列。
[2,3] -> [3,4]接下来,取出队列头的3号状态,我们发现它有两个儿子,在这里标号为5和6,于是借此生成5号和6号状态,加入队列。
![[3,4] -> [4,5,6]](https://haha.school/wp-content/uploads/2015/09/g142.jpeg) [3,4] -> [4,5,6]之后,取出队列头的四号状态,发现在这个状态所在的4号节点有两个儿子,在这里标号7和8,同时据此创建状态并加入队列。
[3,4] -> [4,5,6]之后,取出队列头的四号状态,发现在这个状态所在的4号节点有两个儿子,在这里标号7和8,同时据此创建状态并加入队列。
![[][]](https://haha.school/wp-content/uploads/2015/09/gg.jpeg) [4,5,6] -> [5,6,7,8]最终,队列弹出的5,6,7,8号状态均是在叶子节点的状态,无法创建新状态,队列就此清空,我们完成了遍历任务!来看一下我们整个BFS的全貌吧:
[4,5,6] -> [5,6,7,8]最终,队列弹出的5,6,7,8号状态均是在叶子节点的状态,无法创建新状态,队列就此清空,我们完成了遍历任务!来看一下我们整个BFS的全貌吧:
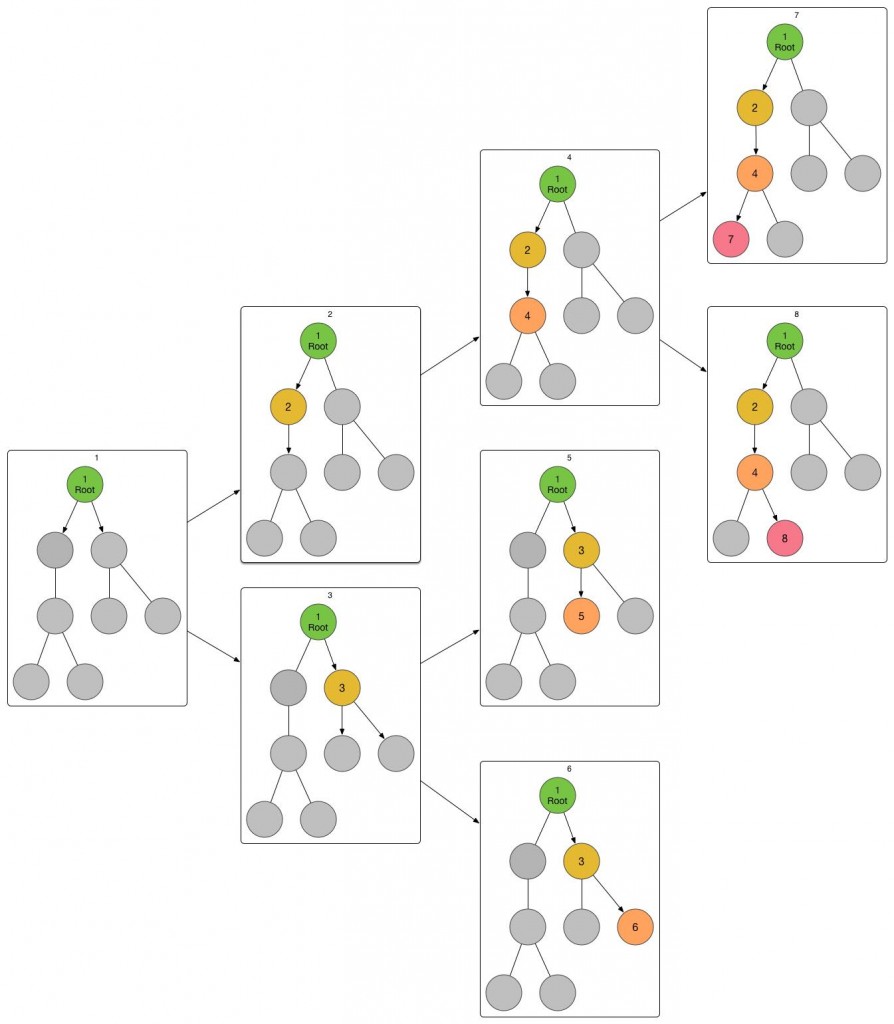 State tree of the whole BFS process
State tree of the whole BFS process
相信你已经可以基本理解BFS的工作方式了。
显然光会个遍历树是不够的,将上面所讲述的思考方式拓展一下,BFS也可以完成“图的遍历”,“迷宫最短路”等问题,下面我会给出一种用于遍历图的BFS实现,图的存储方式采用vector实现的邻接表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
struct Node{ vector<int> to; } vertex[1000]; void addEdge(int from,int to){ vertex[from].to.push_back(to); } bool vis[1000]; void bfs(){ queue<int> que; que.push(1); vis[1] = true; while (!que.empty()) { int now = que.front(); que.pop(); for (int i = 0; i < vertex[now].to.size(); i++) { if (!vis[vertex[now].to[i]]) { que.push(vertex[now].to[i]); vis[vertex[now].to[i]] = true; } } } } |
选择适合的搜索方式
一招鲜显然并不能吃遍天,DFS,BFS中的任何一个都不能应付全部的场合。DFS使用递归实现,因此当搜索深度比较大的时候就存在巨大的栈溢出风险,而实用模拟栈实现的DFS又十分复杂,得不偿失,因此当栈空间不足以支持DFS时,必须换用BFS。BFS相对于DFS,实现相对比较繁琐,如果使用STL queue的话,会带来一些常数上的劣势(这种劣势在SPOJ等黑心OJ上十分明显),模拟队列又可能会占用大量内存。因此我们需要根据问题的实际来考虑使用哪种搜索方式。
一般来说,DFS在求连通性问题上具有十分的优势(Tarjan SCC/DCC算法均基于DFS),而BFS在求最短路问题上占上风(Dijkstra/SPFA算法均基于BFS),掌握好这两种算法是学好图论的基础。如果你够细心的话,你会发现我们在DFS的同时给树进行了编号,那个编号其实叫做“DFI(DFS序)”,这个东西有着一些神奇的应用。同时DFS和BFS又可以升级为一种考虑问题的思想,当然这些高级一些的问题就需要我们在练习的时候慢慢体会了。
本文系hahaschool原创,同时作为Tic ACM Club讲稿,未经许可禁转载。














![[2,3] -> [3,4]](https://haha.school/wp-content/uploads/2015/09/g141.jpeg)
![[3,4] -> [4,5,6]](https://haha.school/wp-content/uploads/2015/09/g142.jpeg)
![[][]](https://haha.school/wp-content/uploads/2015/09/gg.jpeg)