题意
你有一个![]() 大小的棋盘,
大小的棋盘,![]() 行,
行,![]() 列,行号列号都从
列,行号列号都从![]() 开始,行从上到下数到
开始,行从上到下数到![]() ,列从左到右数到
,列从左到右数到![]() ,棋盘的每一个格子可以是黑色或者白色。
,棋盘的每一个格子可以是黑色或者白色。
当满足全部下述条件的时候,认为棋盘上出现了一个”Cave“:
- 存在一个线段
![Rendered by QuickLaTeX.com [l,r] (1 <= l <= r <= n)](https://haha.school/wp-content/ql-cache/quicklatex.com-74242d3d0aa8e8ed2122e7a9f502b612_l3.png) ,使得
,使得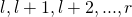 这些行都有且仅有两个黑色格子,其他行不存在黑色格子。
这些行都有且仅有两个黑色格子,其他行不存在黑色格子。 - 存在一个行号
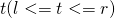 ,使得:
,使得:
- 对于任意存在黑色格子的行
 ,把这行的黑色格子对应的列号和黑色格子之间的列号加入一个集合, 称之为
,把这行的黑色格子对应的列号和黑色格子之间的列号加入一个集合, 称之为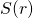 。
。 - 任取t及t之上的两个有黑色格子的行,令上方的行为
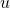 ,下方的行
,下方的行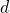 ,则
,则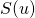 是
是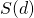 的子集。
的子集。 - 任取
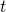 及
及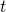 之下的两个有黑色格子的行,令上方的行为
之下的两个有黑色格子的行,令上方的行为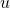 ,下方的行为
,下方的行为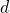 ,则
,则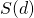 是
是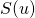 的子集。
的子集。
- 对于任意存在黑色格子的行
你要输出有多少染色的方案,使得棋盘出现一个“Cave”,答案模![]() 。
。
思路
翻译一下题意,就是让我们找一种染色方案,让棋盘上出现下面这样的图案(下图中![]() )。
)。

可以发现,这个图案可以以t行为界分拆为上下两个部分,不妨令![]() 表示得到高度为h的,底部两个黑块宽度必须为w的,每一行都有黑块的,半个图案的染色方案数。
表示得到高度为h的,底部两个黑块宽度必须为w的,每一行都有黑块的,半个图案的染色方案数。
我们可以很容易发现如下的递推关系:
![]()
即:
![]()
考虑同一高度的相邻两项之差:
![]()
这样,我们一行行地计算![]() 的值,一边维护每一行的前缀和,一边算下一项,这样可以用
的值,一边维护每一行的前缀和,一边算下一项,这样可以用![]() 的时间完成预处理。
的时间完成预处理。
接下来我们考虑如何把两个一半的图案合成一个,我们令![]() 表示得到高度为
表示得到高度为![]() ,最宽处宽度为
,最宽处宽度为![]() ,每一行都有黑块的图案的染色方案数,我们有:
,每一行都有黑块的图案的染色方案数,我们有:
![Rendered by QuickLaTeX.com al[h][w] =\sum \left\{\begin{matrix} {hf[1][w] \cdot (2\times hf[h-1][w-1] + 3\times hf[h-1][w-2] + 4\times hf[h-1][w-3] + ... + w\times hf[h-1][1])} \\ {hf[2][w] \cdot (2\times hf[h-2][w-1] + 3\times hf[h-2][w-2] + 4\times hf[h-2][w-3] + ... + w\times hf[h-2][1])} \\ {hf[3][w] \cdot (2\times hf[h-3][w-1] + 3\times hf[h-3][w-2] + 4\times hf[h-3][w-3] + ... + w\times hf[h-3][1])} \\ ... \\ {hf[h][w] \cdot (2\times hf[0][w-1] + 3\times hf[0][w-2] + 4\times hf[0][w-3] + ... + w\times hf[0][1])} \end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-c7e6d3390c11f69f46ca271b4c0859bd_l3.png)
即:
![Rendered by QuickLaTeX.com al[h][w] = \sum \left\{\begin{matrix} hf[1][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[h-1][w-k] \\ hf[2][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[h-2][w-k] \\ hf[3][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[h-3][w-k] \\ ... \\ hf[h][w]\times \sum_{k=1}^{w-1} (k+1)\cdot hf[0][w-k] \end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-cb751eded0c7e38d9a7452d89f308a35_l3.png)
为了让式子更简洁,我们令![]() ,这样的话,我们就有:
,这样的话,我们就有:
![]()
很明显这个式子是一个卷积,如果我们可以预处理出![]() 的值,就可以使用FFT进行快速运算。我们发现
的值,就可以使用FFT进行快速运算。我们发现![]() 的递推关系和
的递推关系和![]() 的递推关系非常相似,我们依然考虑同行相邻两项的差值:
的递推关系非常相似,我们依然考虑同行相邻两项的差值:
![]()
这样我们依然采用一边计算一边维护前缀和的方法,可以在![]() 的时间完成
的时间完成![]() 的预处理。
的预处理。
预处理好![]() 之后,就是计算卷积了,因为题目要求模
之后,就是计算卷积了,因为题目要求模![]() ,我们需要采用NTT+CRT的方式实现任意模空间下的卷积(具体实现原理不是我们的讨论范围),这样的话,在最恶劣情况,我们需要做18000次4096点NTT,单次NTT耗时几毫秒,超时无法避免,我们只能考虑进一步优化。
,我们需要采用NTT+CRT的方式实现任意模空间下的卷积(具体实现原理不是我们的讨论范围),这样的话,在最恶劣情况,我们需要做18000次4096点NTT,单次NTT耗时几毫秒,超时无法避免,我们只能考虑进一步优化。
我们继续考虑,令![]() 表示最宽处宽度为
表示最宽处宽度为![]() ,高度范围在
,高度范围在![]() 的图案,有多少方案可以作成,那么我们有:
的图案,有多少方案可以作成,那么我们有:
![Rendered by QuickLaTeX.com dw[w] = \sum \left\{\begin{matrix} N\cdot al[1][w] \\ (N-1)\cdot al[2][w] \\ (N-2)\cdot al[3][w] \\ ... \\ 1 \cdot al[N][w] \end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-860e88577713d366e9a2e2cca7bdcb11_l3.png)
把![]() 打开,就有:
打开,就有:
![Rendered by QuickLaTeX.com dw[w] = \sum \left\{\begin{matrix} N\times hf[1][w]\cdot rc[0][w] \\ (N-1)\times (hf[1][w]\cdot rc[1][w] + hf[2][w]\cdot rc[0][w]) \\ (N-2)\times (hf[1][w]\cdot rc[2][w] + hf[2][w]\cdot rc[1][w] + hf[3][w]\cdot rc[0][w]) \\ ... \\ 1\times (hf[1][w]\cdot rc[N-1][w] + hf[2][w]\cdot rc[N-2][w] + ... + hf[N][w]\cdot rc[0][w]) \end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-da7f01c212dea7f5d13313685f454a75_l3.png)
我们把![]() 重新整理一下:
重新整理一下:
![Rendered by QuickLaTeX.com dw[w] = \sum \left\{\begin{matrix} hf[1][w]\times (N\cdot rc[0][w] + (N-1)\cdot rc[1][w] + (N-2)\cdot rc[2][w] + ... + 1\cdot rc[N-1][w]) \\ hf[2][w]\times ((N-1)\cdot rc[0][w] + (N-2)\cdot rc[1][w] + (N-3)\cdot rc[2][w] + ... + 1\cdot rc[N-2][w]) \\ hf[3][w]\times ((N-2)\cdot rc[0][w] + (N-3)\cdot rc[1][w] + (N-4)\cdot rc[2][w] + ... + 1\cdot rc[N-3][w]) \\ ... \\ hf[N][w] \times 1 \cdot rc[0][w] \end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-5582fffb95dead1ed52cdc683e471d67_l3.png)
如果比较敏感的话应该已经发现突破口了,我们再整理一下:
![]()
还没看出来?再令![]() ,这样:
,这样:
![]()
而且我们还可以发现![]() 它们的递推关系都是差不多的,也就是说对于
它们的递推关系都是差不多的,也就是说对于![]() 我们继续采用考虑相邻两项差的策略:
我们继续采用考虑相邻两项差的策略:
![]()
这样我们可以用![]() 的时间把
的时间把![]() 搞定,这样的话,计算全部的
搞定,这样的话,计算全部的![]() 的值也是
的值也是![]() 时间了。
时间了。
计算好表示定宽度不定高度的图案数的![]() 之后,接下来我们放宽到不定宽度不定高度的图案数,也就是答案,我们有:
之后,接下来我们放宽到不定宽度不定高度的图案数,也就是答案,我们有:
![]()
这样我们绕了一大圈终于把答案算出来了,总复杂度![]() ,本题至此解决。
,本题至此解决。
实现
NTT+CRT做法
注意这份代码因为常数过大无法通过,但是答案是正确的。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 |
//NTT Version //Warning:Severely Exceeds TL(14s,TL2s),although O(n^2logn) #define REP(i,t) for(int i = 0;i < t; i++) #define REP_1(i,t) for(int i = 1;i <= t; i++) #define CASE_LOOP int ___;scanf(" %d",&___);for(int __ = 1; __ <= ___; __++) #define FOR_EDGE(i,u) for (int i = head[u]; i; i = nxt[i]) #define ADHOC_CIN(typ,name) typ name;cin >> name; #define ADHOC_SCANINT(name) int name;scanf(" %d",&name); using namespace std; typedef long long LL; typedef long double LD; #define USUAL_MODANY #ifdef USUAL_MODANY inline LL getmod(LL a,LL m){if(a<0||a>=m)a%=m;if(a<0)a+=m;return a;} inline LL summod(LL a,LL b,LL m){return getmod(getmod(a,m)+getmod(b,m),m);} inline LL mulmod(LL a,LL b,LL m){return getmod(getmod(a,m)*getmod(b,m),m);} inline LL powmod(LL a,LL p,LL m){LL ret=1;while(p){if(p&1)ret=mulmod(ret,a,m);a=mulmod(a,a,m);p>>=1;}return ret;} inline LL invmod(LL a,LL m){return powmod(a,m-2,m);} #endif #define NTT_MOD_ANY #ifdef NTT_MOD_ANY // 多项式乘法 系数对MOD=1000000007取模, 常数巨大,慎用 // 只要选的K个素数乘积大于MOD*MOD*N,理论上MOD可以任取。 #define MOD 1000000007 #define K 3 //用于CRT的三个模空间 const int m[K] = {1004535809, 998244353, 104857601}; //479*2^21+1,7*17*2^23+1,25*2^22+1 //m[0] > m[1] > m[2] #define G 3 //上述三个素数的原根 const int MAXN = 4444; inline int qpow(int x, int k, int P) { int ret = 1; while(k) { if(k & 1) ret = 1LL * ret * x % P; k >>= 1; x = 1LL * x * x % P; } return ret; } struct _NTT { //wn:旋转分量 P:模空间(P-1是2的幂) int wn[25], P; //init(_P)用给出的模空间_P构建旋转分量 void init(int _P) { P = _P; for(int i = 1; i <= 21; ++i) { int t = 1 << i; wn[i] = qpow(G, (P - 1) / t, P); } } //RADAR编码 //FFT与IFFT之前的反转变换 //位置i和(i的二进制反转)位置互换 //len需要是2的幂 void change(int *y, int len) { for(int i = 1, j = len / 2; i < len - 1; ++i) { if(i < j) swap(y[i], y[j]); int k = len / 2; while(j >= k) { j -= k; k /= 2; } j += k; } } //NTT主过程,y是等待变换的数组,下标从0开始,长度为len //len是2的幂 //on=1的话NTT on=-1的话INTT void NTT(int *y, int len, int on) { change(y, len); int id = 0; for(int h = 2; h <= len; h <<= 1) { ++id; for(int j = 0; j < len; j += h) { int w = 1; for(int k = j; k < j + h / 2; ++k) { int u = y[k]; int t = 1LL * y[k+h/2] * w % P; y[k] = u + t; if(y[k] >= P) y[k] -= P; y[k+h/2] = u - t + P; if(y[k+h/2] >= P) y[k+h/2] -= P; w = 1LL * w * wn[id] % P; } } } if(on == -1) { for(int i = 1; i < len / 2; ++i) swap(y[i], y[len-i]); int inv = qpow(len, P - 2, P); for(int i = 0; i < len; ++i) y[i] = 1LL * y[i] * inv % P; } } //自动多项式乘法,结果将会反映到A数组 //需要事先调整好len至大于离2n最近的2的幂 void mul(int A[], int B[], int len) { NTT(A, len, 1); NTT(B, len, 1); for(int i = 0; i < len; ++i) A[i] = 1LL * A[i] * B[i] % P; NTT(A, len, -1); } }ntt[K]; int tmp[MAXN][K], t1[MAXN], t2[MAXN]; int r[K][K]; //特殊的防爆CRT //x = x0 + x1*p0 + x2*p0*p1 (% p0*p1*p2) [0<=x0<p0 0<=x1<p1 0<=x2<p2] //x = a0 (% p0) //x = a1 (% p1) //x = a2 (% p2) //因为我们保证p0*p1*p2>MODER*MODER*n,在P0*p1*p2模空间内,我们计算的原始数值一定只有单个映射 //我们的目的是求出x0 x1 x2,借此用另外一种形式表达x(p0p1p2混合进制形式) //这样就可以绕开爆LL的问题 //x (%p0) = a0 (%p0) = x0 [因为x0的范围限定在[0,p0),可以看成求出了(% p0*p1*p2)中的x0] //x (%p1) = a1 (%p1) = x0 + x1*p0 (%p1) [因为p1|p0*p1*p2,在大空间中的x0对应到小空间的位置是确定的] // --> x1 = (a1 - x0)/p0 (%p1) [因为x1的范围限定在[0,p1),可以看成求出了(% p0*p1*p2)中的x1] //x (%p2) = a2 (%p2) = x0 + x1*p0 + x2*p0*p1 (%p2) [同上] // --> x2 = (a2 - x0 - x1*p0)/p0*p1 (%p2) [同上] int CRT(int a[]) { int x[K]; for(int i = 0; i < K; ++i) { x[i] = a[i]; for(int j = 0; j < i; ++j) { int t = (x[i] - x[j]) % m[i]; if(t < 0) t += m[i]; x[i] = 1LL * t * r[j][i] % m[i]; } } int mul = 1, ret = x[0] % MOD; for(int i = 1; i < K; ++i) { mul = 1LL * mul * m[i-1] % MOD; ret += 1LL * x[i] * mul % MOD; if(ret >= MOD) ret -= MOD; } return ret; } //自动多项式乘法,模指定的数(1e9+7) //len需要调整到离2n最近的2的幂,下标从0开 //结果存入A[]中 //系数模1e9+7就可以 void mul(int A[], int B[], int len) { for(int id = 0; id < K; ++id) { //转储系数变量 for(int i = 0; i < len; ++i) { t1[i] = A[i]; t2[i] = B[i]; } //使用id号NTT单元做多项式乘法 ntt[id].mul(t1, t2, len); //转储乘法结果 for(int i = 0; i < len; ++i) tmp[i][id] = t1[i]; } //将乘法结果回射到指定(1e9+7)空间 for(int i = 0; i < len; ++i) { A[i] = CRT(tmp[i]); } } //预处理逆元r[i][j]:m[i]在m[j]空间内逆元 //初始化需要的NTT单元 void init() { for(int i = 0; i < K; ++i) { for(int j = 0; j < i; ++j) { r[j][i] = qpow(m[j], m[i] - 2, m[i]); } } for(int i = 0; i < K; ++i) { ntt[i].init(m[i]); } } #endif int N,M; int hf[MAXN/2][MAXN/2]; void prephf2(){ for(int w = 2;w < MAXN/2; w++){ hf[1][w] = 1; } for(int h = 2;h < MAXN/2;h++){ int pfx = 0; for(int w = 1;w < MAXN/2; w++){ pfx = summod(pfx, hf[h-1][w],MOD); hf[h][w] = summod(hf[h][w-1], pfx,MOD); } } } int al[MAXN/2][MAXN/2]; int f[MAXN/2],g[MAXN/2],pfx[MAXN/2]; int ff[MAXN],gg[MAXN]; void prepal2(){ for(int h = 1;h <= 2000; h++){ al[h][2] = 1; } for (int w = 3; w <= 2000; w++) { f[0] = 0; g[0] = 1; for(int h = 1;h <= 2000; h++){ f[h] = hf[h][w]; pfx[h] = summod(pfx[h], hf[h][w-1], MOD); g[h] = summod(summod(pfx[h], g[h], MOD), hf[h][w-1], MOD); } memset(ff, 0, sizeof(ff)); memset(gg, 0, sizeof(gg)); for(int j = 0;j <= 2000; j++){ ff[j] = f[j]; gg[j] = g[j]; } mul(ff, gg, 4096); for(int h = 0;h <= 2000; h++){ al[h][w] = ff[h]; } } } int main(int argc, const char * argv[]){ #ifdef LOCAL_DEBUG freopen("testdata.in", "r", stdin); clock_t clk = clock(); #endif init(); prephf2(); prepal2(); while (cin >> N >> M) { LL res = 0; for(int h = N;h >= 1; h--){ LL mpl = N-h+1; LL tmp = 0; for(int w = M;w >= 2;w--){ LL mlp = M-w+1; tmp = summod(tmp, mulmod(mlp, al[h][w], MOD), MOD); } res = summod(res, mulmod(mpl, tmp, MOD), MOD); } cout << res << endl; } #ifdef LOCAL_DEBUG puts("-----END OF OUTPUT-----"); printf("Time Elapsed: %luMS\n",(clock() - clk)/CLK_TCK/10); #endif return 0; } |
正解
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 |
//Accepted Version //Enumerate w //Enumerate upper part (xxxx5) //preCalculate lower part (4xxx) product times //This can make in O(n^2) time //No NTT required #define REP(i,t) for(int i = 0;i < t; i++) #define REP_1(i,t) for(int i = 1;i <= t; i++) #define CASE_LOOP int ___;scanf(" %d",&___);for(int __ = 1; __ <= ___; __++) #define FOR_EDGE(i,u) for (int i = head[u]; i; i = nxt[i]) #define ADHOC_CIN(typ,name) typ name;cin >> name; #define ADHOC_SCANINT(name) int name;scanf(" %d",&name); using namespace std; typedef long long LL; typedef long double LD; #define USUAL_MOD1E9 #ifdef USUAL_MOD1E9 const LL MODER = 1000000007; LL getmod(LL a){if(a<0||a>=MODER)a%=MODER;if(a<0)a+=MODER;return a;} LL summod(LL a,LL b){return getmod(getmod(a)+getmod(b));} LL mulmod(LL a,LL b){return getmod(getmod(a)*getmod(b));} LL powmod(LL a,LL p){LL ret=1;while(p){if(p&1)ret=mulmod(ret,a);a=mulmod(a,a);p>>=1;}return ret;} LL invmod(LL a){return powmod(a,MODER-2);} #endif const int MAXN = 2005; int N,M; int hf[MAXN][MAXN]; void prephf(){ for(int w = 2;w < MAXN; w++){ hf[1][w] = 1; } for(int h = 2;h < MAXN;h++){ int pfx = 0; for(int w = 1;w < MAXN; w++){ pfx = summod(pfx, hf[h-1][w]); hf[h][w] = summod(hf[h][w-1], pfx); } } } int lower[MAXN][MAXN]; void preplower(){ REP_1(h, MAXN-1){ int pfx = 0; for(int w = 2;w < MAXN; w++){ pfx = summod(pfx, hf[h][w]); lower[h][w] = summod(lower[h][w-1], summod(pfx, hf[h][w])); } } } int sml[MAXN][MAXN]; void prepsml(){ REP_1(w, MAXN-1){ int pfx = 0; REP_1(h, MAXN-1){ pfx = summod(pfx,lower[h][w]); sml[h][w] = summod(sml[h-1][w], pfx); } } } void prep(){ prephf(); preplower(); prepsml(); } void solve(){ int res = 0; REP_1(w, M){ int tim = M+1-w; int tmp = 0; REP_1(upper, N){ tmp = summod(tmp, mulmod(hf[upper][w], (N+1-upper))); tmp = summod(tmp, mulmod(hf[upper][w], sml[N-upper][w-1])); } res = summod(res, mulmod(tmp, tim)); } cout << res << endl; } int main(int argc, const char * argv[]){ #ifdef LOCAL_DEBUG freopen("testdata.in", "r", stdin); clock_t clk = clock(); #endif prep(); while (cin >> N >> M) { solve(); } #ifdef LOCAL_DEBUG puts("-----END OF OUTPUT-----"); printf("Time Elapsed: %luMS\n",(clock() - clk)/CLK_TCK/10); #endif return 0; } |
参考
- kmjpさん(日本語注意):
http://kmjp.hatenablog.jp/entry/2014/09/22/0900- Zeyu_king:
http://blog.csdn.net/zeyu_king/article/details/44040749