题意
给你一颗树,上面有黑点(母体机器人所在位置),有白点(没有潜伏母体机器人的安全节点),并且给了你每一条边的边权(删边(炸毁道路)需要的时间代价)。现在要你以最小代价删掉一些边,使得没有两个黑点同时可以互相连通。输出这个时间花费即可。
思路
树形DP。这个题和Codeforces 461B Appleman and Tree是一个路子的题,都是在一棵树上不允许同时出现两个联通的特定类别的节点。这种问题我们在思考的时候,方向是将当前的大问题分解成同样的小问题,不断分解到最后,然后考虑怎么样根据一些小问题解得出大问题的解,这是DP的思路所在。
这次,我们设状态表示为![]() ,其中
,其中![]() 表示要想让以
表示要想让以![]() 为根节点的子树满足题目的要求,而且a所在的联通块里面不可以有黑点,需要的最小代价是多少;
为根节点的子树满足题目的要求,而且a所在的联通块里面不可以有黑点,需要的最小代价是多少;![]() 表示要想让以
表示要想让以![]() 为根节点的子树满足题目要求,且
为根节点的子树满足题目要求,且![]() 所在的联通块里面有且只有一个黑点,需要的最小代价是多少。
所在的联通块里面有且只有一个黑点,需要的最小代价是多少。
设好了状态,我们开始想DP方程:
- 我们当前检查的点标号是
 ,我们去逐一检查他的孩子节点,标号是
,我们去逐一检查他的孩子节点,标号是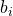 ,如果a是一个黑点:
,如果a是一个黑点:
![Rendered by QuickLaTeX.com dp[a][1] = \sum\min \left\{\begin{matrix}dp[b_{i}][0]\\ dp[b_{i}][0]+cost(a \rightarrow b_{i})\\ dp[b_{i}][1]+cost(a \rightarrow b_{i})\end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-16a9a5a93828d71a325e2ae145159a4b_l3.png)
因为当前节点是黑点,我们有三种操作可以选:- 当前讨论的孩子部分,如果他没有与任何黑点连着,我们可以把这个部分连入当前讨论的根部分,这就是
![Rendered by QuickLaTeX.com dp[b_{i}][0]](https://haha.school/wp-content/ql-cache/quicklatex.com-766930a6e3c46d9087c04b15b813689f_l3.png) ,即孩子的代价就是根的代价,因为没有切断就没有增加代价。
,即孩子的代价就是根的代价,因为没有切断就没有增加代价。 - 把根部分和当前讨论的孩子部分中间的边切断,这样的话无论孩子部分到底有没有和黑点连接,都没有关系,只要把孩子的代价加上切断代价就是这样做的代价了,也就是
![Rendered by QuickLaTeX.com dp[b_{i}][0]+cost(a \rightarrow b_{i})](https://haha.school/wp-content/ql-cache/quicklatex.com-2875abcec94185fa88087754d25e1aa2_l3.png) (孩子部分没有和黑点相连的情况下切断)和
(孩子部分没有和黑点相连的情况下切断)和![Rendered by QuickLaTeX.com dp[b_{i}][1]+cost(a \rightarrow b_{i})](https://haha.school/wp-content/ql-cache/quicklatex.com-50a20d7b9e0cd4518e1c698e4a551476_l3.png) (孩子部分有和黑点相连的情况下切断)。
(孩子部分有和黑点相连的情况下切断)。 - 比较这三种选择,取最优就是局部最优解了。
- 当前讨论的孩子部分,如果他没有与任何黑点连着,我们可以把这个部分连入当前讨论的根部分,这就是
![Rendered by QuickLaTeX.com dp[a][0]=\inf](https://haha.school/wp-content/ql-cache/quicklatex.com-6ee03f42e22977937b0fbd1e70e46bb9_l3.png)
黑点不可能不和黑点相连,所以这里用inf屏蔽掉这种选择。
- 如果a是一个白点:
![Rendered by QuickLaTeX.com dp[a][1] = \min \left\{\begin{matrix}dp[a][0]+dp[b_{i}][1]\\ dp[a][1]+dp[b_{i}][0]\\ dp[a][1]+dp[b_{i}][1]+cost(a\rightarrow b_{i})\\ dp[a][1]+dp[b_{i}][0]+cost(a\rightarrow b_{i})\end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-44f243d24f72f7f10945e03b95c91f63_l3.png)
因为当前节点是白色,我们想要让他变成连着黑色的情况,这样的话有四种操作可以选:- 假如截止目前和根部连接的所有孩子都不包含黑点,我们可以让现在的这个孩子部分以含有黑点的形态和根部连接,使根部变成有黑点的情况。这就是
![Rendered by QuickLaTeX.com dp[a][0]+dp[b_{i}][1]](https://haha.school/wp-content/ql-cache/quicklatex.com-1a0ca9122bce2026e217d38f96396a44_l3.png) 。
。 - 假如当前的根部已经连有黑点,为了满足要求,新联入的部分不可以再包含黑点,这就是
![Rendered by QuickLaTeX.com dp[a][1]+dp[b_{i}][0]](https://haha.school/wp-content/ql-cache/quicklatex.com-a362d8492209940cf5bf281a10c4f4e2_l3.png) .
. - 假如孩子部分被切断,这样的话就无所谓孩子长成啥样了,只要算一下代价就可以了,也就是
![Rendered by QuickLaTeX.com dp[b_{i}][0]+cost(a \rightarrow b_{i})](https://haha.school/wp-content/ql-cache/quicklatex.com-2875abcec94185fa88087754d25e1aa2_l3.png) (孩子部分没有和黑点相连的情况下切断)和
(孩子部分没有和黑点相连的情况下切断)和![Rendered by QuickLaTeX.com dp[b_{i}][1]+cost(a \rightarrow b_{i})](https://haha.school/wp-content/ql-cache/quicklatex.com-50a20d7b9e0cd4518e1c698e4a551476_l3.png) (孩子部分有和黑点相连的情况下切断)。
(孩子部分有和黑点相连的情况下切断)。 - 这四种选择里面选最优的就好了。
- 假如截止目前和根部连接的所有孩子都不包含黑点,我们可以让现在的这个孩子部分以含有黑点的形态和根部连接,使根部变成有黑点的情况。这就是
![Rendered by QuickLaTeX.com dp[a][0] = \sum\min \left\{\begin{matrix}dp[b_{i}][0]\\ dp[b_{i}][0]+cost(a \rightarrow b_{i})\\ dp[b_{i}][1]+cost(a \rightarrow b_{i})\end{matrix}\right.](https://haha.school/wp-content/ql-cache/quicklatex.com-cd6d322e0ff50f3b5f36791ba0bbed20_l3.png)
当前节点是白色,我们想要让她不要根任何黑色连上,这样的话有3种选择:- 当前讨论的孩子部分没有和黑色连着,我们可以放心的把这部分连到根部,这就是
![Rendered by QuickLaTeX.com dp[b_{i}][0]](https://haha.school/wp-content/ql-cache/quicklatex.com-766930a6e3c46d9087c04b15b813689f_l3.png) 。
。 - 切断了和孩子部分之间的连接,也就是
![Rendered by QuickLaTeX.com dp[b_{i}][0]+cost(a \rightarrow b_{i})](https://haha.school/wp-content/ql-cache/quicklatex.com-2875abcec94185fa88087754d25e1aa2_l3.png) (孩子部分没有和黑点相连的情况下切断)和
(孩子部分没有和黑点相连的情况下切断)和![Rendered by QuickLaTeX.com dp[b_{i}][1]+cost(a \rightarrow b_{i})](https://haha.school/wp-content/ql-cache/quicklatex.com-50a20d7b9e0cd4518e1c698e4a551476_l3.png) (孩子部分有和黑点相连的情况下切断)。(其实我已经复制了这一段两遍。。。)
(孩子部分有和黑点相连的情况下切断)。(其实我已经复制了这一段两遍。。。)
- 当前讨论的孩子部分没有和黑色连着,我们可以放心的把这部分连到根部,这就是
- 注意这两个
![Rendered by QuickLaTeX.com dp[a][0]](https://haha.school/wp-content/ql-cache/quicklatex.com-1725e30e898b612827f3f7c59014e489_l3.png) 和
和![Rendered by QuickLaTeX.com dp[a][1]](https://haha.school/wp-content/ql-cache/quicklatex.com-106198b084b4e4c4ef147bfd42db3b55_l3.png) 要同时处理,因为这里面有一个从“刚才”
要同时处理,因为这里面有一个从“刚才”![Rendered by QuickLaTeX.com dp[a][0]](https://haha.school/wp-content/ql-cache/quicklatex.com-1725e30e898b612827f3f7c59014e489_l3.png) 到“现在”
到“现在”![Rendered by QuickLaTeX.com dp[a][1]](https://haha.school/wp-content/ql-cache/quicklatex.com-106198b084b4e4c4ef147bfd42db3b55_l3.png) 的转移。
的转移。
方程想好之后,DFS深入叶子部分,在返回的时候处理好![]() 数组就可以了,最后我们要在
数组就可以了,最后我们要在![]() 和
和![]() 之间取个最小的,因为你所制定的根在最优解的时候连不连黑点并不知道。
之间取个最小的,因为你所制定的根在最优解的时候连不连黑点并不知道。
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 |
#include <iostream> #include <algorithm> #include <queue> #include <vector> #include <cstdlib> #include <cstdio> #include <string> #include <cstring> #include <ctime> #include <iomanip> #include <cmath> #include <set> #include <stack> #include <cmath> #include <map> using namespace std; static long long MAXN = 909303909303; struct nodeType{ vector<int> to; vector<int> cost; int color; } vertex[100005]; void addEdge(int from,int to,int cost){ vertex[from].to.push_back(to); vertex[from].cost.push_back(cost); } long long dp[100005][2]; void dfs(int cur, int par){ nodeType &currNode = vertex[cur]; for (int i = 0; i < currNode.to.size(); i++) { if (currNode.to[i] != par) { dfs(currNode.to[i], cur); } } if (currNode.color == 1) { dp[cur][0] = MAXN; dp[cur][1] = 0; for (int i = 0; i < currNode.to.size(); i++) { if (currNode.to[i] != par) { dp[cur][1] += min(dp[currNode.to[i]][0],min(dp[currNode.to[i]][0]+currNode.cost[i], dp[currNode.to[i]][1]+currNode.cost[i])); } } }else { dp[cur][0] = 0; dp[cur][1] = 0; for (int i = 0; i < currNode.to.size(); i++) { if (currNode.to[i] != par) { dp[cur][1] = min(dp[cur][0]+dp[currNode.to[i]][1], min(dp[cur][1]+dp[currNode.to[i]][0],min(dp[cur][1]+dp[currNode.to[i]][0]+currNode.cost[i], dp[cur][1]+dp[currNode.to[i]][1]+currNode.cost[i]))); dp[cur][0] += min(dp[currNode.to[i]][0], min(dp[currNode.to[i]][0]+currNode.cost[i], dp[currNode.to[i]][1]+currNode.cost[i])); } } } } int main(){ int caseCnt = 0; scanf(" %d",&caseCnt); while (caseCnt--) { int n = 0,k = 0; scanf(" %d %d",&n,&k); for (int i = 0; i < n; i++) { //init vertex[i].to.clear(); vertex[i].cost.clear(); vertex[i].color = 0; } for (int i = 0; i < n-1; i++) { int a = 0,b = 0,c = 0; scanf(" %d %d %d",&a,&b,&c); addEdge(a, b, c); addEdge(b, a, c); } for (int i = 0; i < k; i++) { int blkpt = 0; scanf(" %d",&blkpt); vertex[blkpt].color = 1; } dfs(0, -1); cout << min(dp[0][0], dp[0][1]) << endl; } return 0; } |